题目内容
3.因式分解(1)(2x-1)2-(4x+3)2=-4(3x+1)(x+2).
(2)4(x+2y)2-25=(2x+4y+5)(2x+4y-5).
(3)x4-81=(x2+9)(x+3)(x-3).
(4)5x2+16x+12=(5x+6)(x+2).
分析 (1)原式利用平方差公式分解即可;
(2)原式利用平方差公式分解即可;
(3)原式利用平方差公式分解即可;
(4)原式利用十字相乘法分解即可.
解答 解:(1)原式=[(2x-1)+(4x+3)][(2x-1)-(4x+3)]=-4(3x+1)(x+2);
(2)原式=[2(x+2y)+5][2(x+2y)-5]=(2x+4y+5)(2x+4y-5);
(3)原式=(x2-9)(x2+9)=(x2+9)(x+3)(x-3);
(4)原式=(5x+6)(x+2).
故答案为:(1)-4(3x+1)(x+2);(2)(2x+4y+5)(2x+4y-5);(3)(x2+9)(x+3)(x-3);(4)(5x+6)(x+2)
点评 此题考查了因式分解-十字相乘法,以及运用公式法,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.在“走基层,树新风”活动中,青年记者深入边远山区,随机走访农户,调查农村儿童生活教育现状.根据收集的数据,编制了不完整的统计图表如下:
山区儿童生活教育现状
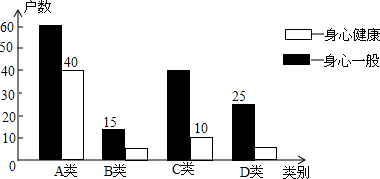
请你用学过的统计知识,解决问题:
(1)记者走访了边远山区多少家农户?
(2)将统计表中的空缺数据填写完整;
(3)分析数据后,你能得出什么结论?
山区儿童生活教育现状
| 类别 | 现状 | 户数 | 比例 |
| A类 | 父母常年在外打工,孩子留在老家由老人照顾 | 100 | |
| B类 | 父母常年在外打工,孩子带在身边 | 20 | 10% |
| C类 | 父母就近在城镇打工,晚上回家照顾孩子 | 50 | |
| D类 | 父母在家务农,并照顾孩子 | 15% |

请你用学过的统计知识,解决问题:
(1)记者走访了边远山区多少家农户?
(2)将统计表中的空缺数据填写完整;
(3)分析数据后,你能得出什么结论?
8.已知抛物线y=ax2与直线y=3x-2都经过点P(2,b).
(1)求a,b的值;
(2)一条开口向下,顶点为原点,且对称轴为y轴的抛物线恰好经过点M(2a,2a-b),求这条抛物线对应的函数表达式.
(1)求a,b的值;
(2)一条开口向下,顶点为原点,且对称轴为y轴的抛物线恰好经过点M(2a,2a-b),求这条抛物线对应的函数表达式.
12.书架上有3本小说、2本散文,从中随机抽取2本都是小说的概率是( )
| A. | $\frac{3}{10}$ | B. | $\frac{6}{25}$ | C. | $\frac{9}{25}$ | D. | $\frac{3}{5}$ |
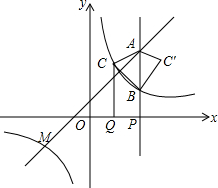 如图,点M(-3,m)是一次函数y=x+1与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一个交点.
如图,点M(-3,m)是一次函数y=x+1与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一个交点.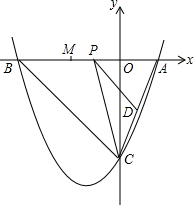 已知:如图,抛物线y=a(x+1)2+c与y轴交于点C(0,-4),与x轴交于点A、B,点A的坐标为(2,0).
已知:如图,抛物线y=a(x+1)2+c与y轴交于点C(0,-4),与x轴交于点A、B,点A的坐标为(2,0).