题目内容
19.把长为36cm的铁丝剪成相等的两段,用一段弯成一个矩形,另一段弯成一个有一条边为5cm的等腰三角形,如果矩形的面积与等腰三角形面积相等,求矩形的长和宽.分析 根据题意求出矩形和等腰三角形的周长,分等腰三角形的腰为5cm和等腰三角形的底为5cm两种情况进行解答即可.
解答 解:由题意得,矩形和等腰三角形的周长都是18cm,
当等腰三角形的腰为5cm时,底边长为8cm,则三角形的面积为12cm2,
设矩形的长为x,则宽为9-x,
x(9-x)=12,
解得,x1=$\frac{9+\sqrt{33}}{2}$,x2=$\frac{9-\sqrt{33}}{2}$,
9-x1=$\frac{9-\sqrt{33}}{2}$,9-x2=$\frac{9+\sqrt{33}}{2}$,
则矩形的长和宽分别为$\frac{9+\sqrt{33}}{2}$,$\frac{9-\sqrt{33}}{2}$;
当等腰三角形的底为5cm时,腰长为6.5cm,则三角形的面积为15cm2,
设矩形的长为x,则宽为9-x,
x(9-x)=15,
解得,x1=$\frac{9+\sqrt{21}}{2}$,x2=$\frac{9-\sqrt{21}}{2}$,
9-x1=$\frac{9-\sqrt{21}}{2}$,9-x2=$\frac{9+\sqrt{21}}{2}$,
则矩形的长和宽分别为$\frac{9+\sqrt{21}}{2}$,$\frac{9-\sqrt{21}}{2}$.
点评 本题考查的是等腰三角形的性质和列一元二次方程解应用题,根据题意正确找出等量关系,列出方程、正确解出方程是解题的关键,注意分情况讨论思想的运用.

练习册系列答案
相关题目
9.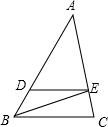 如图,在△ABC中,DE∥BC,∠DBE=30°,∠EBC=25°,则∠ADE为( )
如图,在△ABC中,DE∥BC,∠DBE=30°,∠EBC=25°,则∠ADE为( )
 如图,在△ABC中,DE∥BC,∠DBE=30°,∠EBC=25°,则∠ADE为( )
如图,在△ABC中,DE∥BC,∠DBE=30°,∠EBC=25°,则∠ADE为( )| A. | 65° | B. | 55° | C. | 45° | D. | 75° |
7.菱形和矩形一定具备的性质是( )
| A. | 对角线互相平分 | B. | 对角线互相垂直 | ||
| C. | 对角线相等 | D. | 每条对角线平分一组对角 |
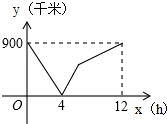 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,两车的距离y(千米)与慢车行驶的时间为x(小时)之间的函数关系如图所示,则快车到达乙地时慢车离乙地距离为450千米.
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,两车的距离y(千米)与慢车行驶的时间为x(小时)之间的函数关系如图所示,则快车到达乙地时慢车离乙地距离为450千米.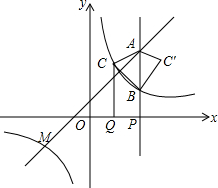 如图,点M(-3,m)是一次函数y=x+1与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一个交点.
如图,点M(-3,m)是一次函数y=x+1与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一个交点.