题目内容
13.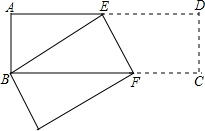 如图,在长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
如图,在长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )| A. | 6cm2 | B. | 8cm2 | C. | 10cm2 | D. | 12cm2 |
分析 首先根据翻折的性质得到ED=BE,再设出未知数,分别表示出线段AE,ED,BE的长度,然后在Rt△ABE中利用勾股定理求出AE的长度,进而求出AE的长度,就可以利用面积公式求得△ABE的面积了.
解答 解:∵长方形折叠,使点B与点D重合,
∴ED=BE,
设AE=xcm,则ED=BE=(9-x)cm,
在Rt△ABE中,
AB2+AE2=BE2,
∴32+x2=(9-x)2,
解得:x=4,
∴△ABE的面积为:3×4×$\frac{1}{2}$=6(cm2).
故选:A.
点评 此题主要考查了图形的翻折变换和学生的空间想象能力,解题过程中应注意折叠后哪些线段是重合的,相等的,如果想象不出哪些线段相等,可以动手折叠一下即可.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
1.下列运算正确的是( )
| A. | 4$\sqrt{3}$-3$\sqrt{3}$=1 | B. | $\sqrt{2}$$+\sqrt{3}$=$\sqrt{5}$ | C. | $\frac{\sqrt{8}}{\sqrt{2}}$=2 | D. | $\sqrt{(-3)^{2}}$=-3 |
18.⊙O中,∠AOB=80°,若C是⊙O上一点(不与A、B重合),则∠ACB等于( )
| A. | 40° | B. | 80° | C. | 80°或100° | D. | 40°或140° |
5.若xa=3,xb=5,则x3a-2b的值为( )
| A. | $\frac{27}{25}$ | B. | $\frac{3}{5}$ | C. | 2 | D. | 52 |
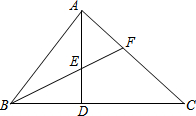 在直角△ABC中,∠BAC=90°,BF平分∠ABC,∠AEF=∠AFE.
在直角△ABC中,∠BAC=90°,BF平分∠ABC,∠AEF=∠AFE.