题目内容
3.计算:$\sqrt{18}$-$\sqrt{\frac{9}{2}}$=$\frac{3\sqrt{2}}{2}$.分析 先把各根式化为最减二次根式,再合并同类项即可.
解答 解:原式=3$\sqrt{2}$-$\frac{3\sqrt{2}}{2}$
=$\frac{3\sqrt{2}}{2}$.
故答案为:$\frac{3\sqrt{2}}{2}$.
点评 本题考查的是二次根式的加减法,熟知二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.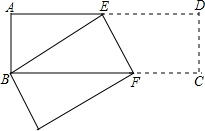 如图,在长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
如图,在长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
 如图,在长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
如图,在长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )| A. | 6cm2 | B. | 8cm2 | C. | 10cm2 | D. | 12cm2 |
12.在数轴上点A表示-4,如果把原点O向正方向移动1个单位,那么在新数轴上点A表示的数是( )
| A. | -5 | B. | -4 | C. | -3 | D. | -2 |
 如图,已知直线y=ax+b经过点A(0,-3),与x轴交于点C,且与双曲线相交于点B(-4,1).
如图,已知直线y=ax+b经过点A(0,-3),与x轴交于点C,且与双曲线相交于点B(-4,1). 如图,已知一个几何体的三视图和有关的尺寸如图所示,请写出该几何体的形状,并根据图中所给的数据求出表面积.
如图,已知一个几何体的三视图和有关的尺寸如图所示,请写出该几何体的形状,并根据图中所给的数据求出表面积.