题目内容
10.已知二次函数y=-x2+(m-1)x+1,当x<1时,y随x的增大而增大,则m的取值范图是( )| A. | m≥3 | B. | m>3 | C. | m≤-1 | D. | m<-1 |
分析 根据a=-1可得知抛物线的开口朝下,由“当x<1时,y随x的增大而增大”可得出抛物线的对称轴x≥1,结合给定二次函数解析式利用抛物线的对称轴为x=-$\frac{b}{2a}$,可得出关于m的一元一次不等式,解不等式即可得出结论.
解答 解:∵a=-1<0,
∴抛物线的开口向下,
又∵当x<1时,y随x的增大而增大,
∴抛物线的对称轴x≥1.
∵二次函数的解析式为y=-x2+(m-1)x+1,
∴抛物线的对称轴为x=-$\frac{m-1}{2×(-1)}$=$\frac{m-1}{2}$≥1,
解得:m≥3.
故选A.
点评 本题考查了二次函数的性质以及解一元一次不等式,解题的关键是根据单调性结合二次函数的性质得出关于m的一元一次不等式.本题属于基础题,难度不大,解决该题型题目时,根据给定的单调区间确定对称轴的范围是关键.

练习册系列答案
相关题目
19.一个正数的算术根为m,则比这个数大2的数的算术平方根是( )
| A. | $\sqrt{{m}^{2}+2}$ | B. | $\sqrt{m+2}$ | C. | m2+2 | D. | m+2 |
20.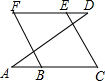 如图,能够判断FB∥CE的条件是( )
如图,能够判断FB∥CE的条件是( )
 如图,能够判断FB∥CE的条件是( )
如图,能够判断FB∥CE的条件是( )| A. | ∠F+∠C=180° | B. | ∠ABF=∠C | C. | ∠F=∠C | D. | ∠A=∠D |
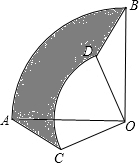 把两个圆心角是90°的扇形OAB与OCD如图那样叠放在一起,连接AC、BD.
把两个圆心角是90°的扇形OAB与OCD如图那样叠放在一起,连接AC、BD.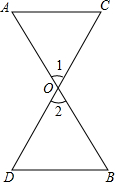 如图所示,AB,CD相交于点O,∠A=∠1,∠B=∠2,AC与BD平行吗?为什么?
如图所示,AB,CD相交于点O,∠A=∠1,∠B=∠2,AC与BD平行吗?为什么? 如图所示,已知直线a,b,c,d,e,b∥c,且∠1=∠2,a与c平行吗?说明理由.
如图所示,已知直线a,b,c,d,e,b∥c,且∠1=∠2,a与c平行吗?说明理由.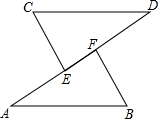 如图所示,AB∥CD,∠CEA=3∠A,∠BFD=3∠D,试说明:CE∥BF.
如图所示,AB∥CD,∠CEA=3∠A,∠BFD=3∠D,试说明:CE∥BF.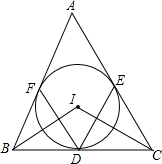 如图,△ABC中,内切圆I和边BC,CA,AB分别相切于点D,F,求证:
如图,△ABC中,内切圆I和边BC,CA,AB分别相切于点D,F,求证: