题目内容
14. 如图,AB为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为$\frac{4}{3}π-\sqrt{3}$.(结果保留π)
如图,AB为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为$\frac{4}{3}π-\sqrt{3}$.(结果保留π)
分析 过O点作OE⊥CD于E,首先根据切线的性质和直角三角形的性质可得∠AOB=60°,再根据平角的定义和三角形外角的性质可得∠COD=120°,∠OCD=∠ODC=30°,根据含30°的直角三角形的性质可得OE,CD的长,再根据阴影部分的面积=扇形OCD的面积-三角形OCD的面积,列式计算即可求解.
解答 解:过O点作OE⊥CD于E,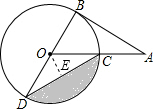
∵AB为⊙O的切线,
∴∠ABO=90°,
∵∠A=30°,
∴∠AOB=60°,
∴∠COD=120°,∠OCD=∠ODC=30°,
∵⊙O的半径为2,
∴OE=1,CE=DE=$\sqrt{3}$,
∴CD=2$\sqrt{3}$,
∴图中阴影部分的面积为:$\frac{120π×{2}^{2}}{360}-\frac{1}{2}×2\sqrt{3}×1=\frac{4}{3}π-\sqrt{3}$.
故答案为:$\frac{4}{3}π-\sqrt{3}$.
点评 考查了扇形面积的计算,切线的性质,本题关键是理解阴影部分的面积=扇形OCD的面积-三角形OCD的面积.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
19.一个正数的算术根为m,则比这个数大2的数的算术平方根是( )
| A. | $\sqrt{{m}^{2}+2}$ | B. | $\sqrt{m+2}$ | C. | m2+2 | D. | m+2 |
3. 如图,在?ABCD中,AD=4cm,AB=2cm,则?ABCD的周长是( )
如图,在?ABCD中,AD=4cm,AB=2cm,则?ABCD的周长是( )
 如图,在?ABCD中,AD=4cm,AB=2cm,则?ABCD的周长是( )
如图,在?ABCD中,AD=4cm,AB=2cm,则?ABCD的周长是( )| A. | 12cm | B. | 10cm | C. | 8cm | D. | 6cm |
4.下列计算错误的是( )
| A. | a8÷a4=a4 | B. | (-a)5÷(-a)4=-a | C. | (-a)5÷(-a4)=a | D. | (b-a)3÷(a-b)2=a-b |
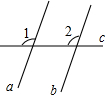 同位角相等,两直线平行.符号语言:(如图)∵∠1=∠2(已知)∴a∥b(同位角相等,两直线平行)
同位角相等,两直线平行.符号语言:(如图)∵∠1=∠2(已知)∴a∥b(同位角相等,两直线平行)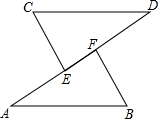 如图所示,AB∥CD,∠CEA=3∠A,∠BFD=3∠D,试说明:CE∥BF.
如图所示,AB∥CD,∠CEA=3∠A,∠BFD=3∠D,试说明:CE∥BF.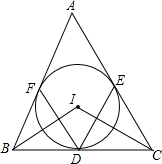 如图,△ABC中,内切圆I和边BC,CA,AB分别相切于点D,F,求证:
如图,△ABC中,内切圆I和边BC,CA,AB分别相切于点D,F,求证: