题目内容
3.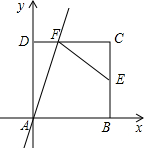 如图,正方形ABCD的边长为2,A为坐标原点,AB和AD分别在x轴、y轴上,点E是BC边的中点,过点A的直线y=kx交线段DC于点F,连接EF,若AF平分∠DFE,则k的值为1或3.
如图,正方形ABCD的边长为2,A为坐标原点,AB和AD分别在x轴、y轴上,点E是BC边的中点,过点A的直线y=kx交线段DC于点F,连接EF,若AF平分∠DFE,则k的值为1或3.
分析 分两种情况:①当点F在DC之间时,作出辅助线,求出点F的坐标即可求出k的值;②当点F与点C重合时求出点F的坐标即可求出k的值.
解答 解:①如图,作AG⊥EF交EF于点G,连接AE,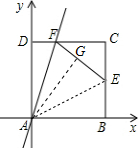
∵AF平分∠DFE,
∴DF=AG=2,
在RT△ADF和RT△AGF中,
$\left\{\begin{array}{l}{DF=AG}\\{AF=AF}\end{array}\right.$,
∴RT△ADF≌RT△AGF(HL),
∴DF=FG,
∵点E是BC边的中点,
∴BE=CE=1,
∴AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{5}$,
∴GE=$\sqrt{A{E}^{2}-A{G}^{2}}$=1,
∴在RT△FCE中,EF2=FC2+CE2,即(DF+1)2=(2-DF)2+1,解得DF=$\frac{2}{3}$,
∴点F($\frac{2}{3}$,2),
把点F的坐标代入y=kx得:2=$\frac{2}{3}$k,解得k=3;
②当点F与点C重合时,
∵四边形ABCD是正方形,
∴AF平分∠DFE,
∴F(2,2),
把点F的坐标代入y=kx得:2=2k,解得k=1.
故答案为:1或3.
点评 本题主要考查了一次函数综合题,涉及角平分线的性质,三角形全等的判定及性质,正方形的性质理,及勾股定解题的关键是分两种情况求出k.

练习册系列答案
相关题目
14.下列运算中,正确的是( )
| A. | (-a2b3)2=a4b6 | B. | (-2a)2=-4a2 | C. | (a+b)2=a2+b2 | D. | b2•b3=2b3 |
11.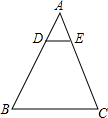 如图,在△ABC中,DE∥BC,$\frac{AD}{DB}=\frac{1}{2}$,DE=4,则BC的长( )
如图,在△ABC中,DE∥BC,$\frac{AD}{DB}=\frac{1}{2}$,DE=4,则BC的长( )
 如图,在△ABC中,DE∥BC,$\frac{AD}{DB}=\frac{1}{2}$,DE=4,则BC的长( )
如图,在△ABC中,DE∥BC,$\frac{AD}{DB}=\frac{1}{2}$,DE=4,则BC的长( )| A. | 8 | B. | 10 | C. | 12 | D. | 16 |
18.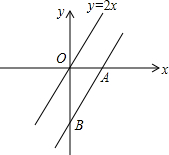 如图,把直线y=2x向下平移后得到直线AB,直线AB与x轴、y轴分别相交于点A、B.若△ABO的面积是1,则直线AB的解析式是( )
如图,把直线y=2x向下平移后得到直线AB,直线AB与x轴、y轴分别相交于点A、B.若△ABO的面积是1,则直线AB的解析式是( )
 如图,把直线y=2x向下平移后得到直线AB,直线AB与x轴、y轴分别相交于点A、B.若△ABO的面积是1,则直线AB的解析式是( )
如图,把直线y=2x向下平移后得到直线AB,直线AB与x轴、y轴分别相交于点A、B.若△ABO的面积是1,则直线AB的解析式是( )| A. | y=3x+$\sqrt{2}$ | B. | y=2x-$\sqrt{2}$ | C. | y=3x-2 | D. | y=2x-2 |
8.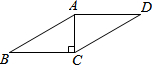 如图,在?ABCD中,过A点作高,垂足刚好为点C,AC=2,∠B=30°,则?ABCD的周长是( )
如图,在?ABCD中,过A点作高,垂足刚好为点C,AC=2,∠B=30°,则?ABCD的周长是( )
 如图,在?ABCD中,过A点作高,垂足刚好为点C,AC=2,∠B=30°,则?ABCD的周长是( )
如图,在?ABCD中,过A点作高,垂足刚好为点C,AC=2,∠B=30°,则?ABCD的周长是( )| A. | $8+4\sqrt{3}$ | B. | $4+2\sqrt{3}$ | C. | 8 | D. | 4 |
15.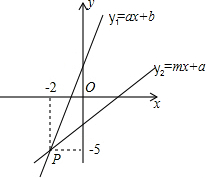 如图,已知一次函数y1=ax+b(a≠0)和y2=mx+n(n≠0)的图象交于点P(-2,-5),则不等式ax+b>mx+n的解集是( )
如图,已知一次函数y1=ax+b(a≠0)和y2=mx+n(n≠0)的图象交于点P(-2,-5),则不等式ax+b>mx+n的解集是( )
 如图,已知一次函数y1=ax+b(a≠0)和y2=mx+n(n≠0)的图象交于点P(-2,-5),则不等式ax+b>mx+n的解集是( )
如图,已知一次函数y1=ax+b(a≠0)和y2=mx+n(n≠0)的图象交于点P(-2,-5),则不等式ax+b>mx+n的解集是( )| A. | x>-5 | B. | x>-2 | C. | x<-2 | D. | x<-5 |