题目内容
13.解方程:(1)3x2-x-1=0
(2)(2x+3)2=(x-1)2.
分析 (1)先求出b2-4ac的值,再代入公式求出即可.
(2)方程右边化为0,左边化为积的形式,然后利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.
解答 解:(1)3x2-x-1=0,
∵a=3,b=-1,c=-1,
∴b2-4ac=(-1)2-4×3×(-1)=13,
∴x=$\frac{1±\sqrt{13}}{2×3}$=$\frac{1±\sqrt{13}}{6}$,
∴x1=$\frac{1+\sqrt{13}}{6}$,x2=$\frac{1-\sqrt{13}}{6}$.
(2)(2x+3)2=(x-1)2.
方程变形得:(2x+3)2-(x-1)2=0,
分解因式得:(2x+3+x-1)(2x+3-x+1)=0,
∴2x+3+x-1=0,2x+3-x+1=0,
∴x1=-$\frac{2}{3}$,x2=-4.
点评 本题考查了解一元二方程的应用,主要考查学生能否正确运用公式法和因式分解法解一元二次方程.

练习册系列答案
相关题目
4.给出下列函数:①y=2x-1;②y=$\frac{1}{x}$;③y=-2x2.从中任取一个函数,取出的函数符合条件“当x>1时,函数值y随x增大而减小”的概率是( )
| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 0 |
1.$\sqrt{x+1}$在实数范围内有意义,则x应满足的条件是( )
| A. | x>1 | B. | x≥1 | C. | x>-1 | D. | x≥-1 |
8.在多边形内角和公式的探究过程中,主要运用的数学思想是( )
| A. | 化归思想 | B. | 分类讨论 | C. | 方程思想 | D. | 数形结合思想 |
18.甲型H7N9流感典型性病毒的直径约为0.00000156米,则此数用科学记数法可表示为( )
| A. | 15.6×10-5 | B. | 1.56×10-5 | C. | 1.56×10-6 | D. | 0.156×10-8 |
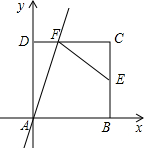 如图,正方形ABCD的边长为2,A为坐标原点,AB和AD分别在x轴、y轴上,点E是BC边的中点,过点A的直线y=kx交线段DC于点F,连接EF,若AF平分∠DFE,则k的值为1或3.
如图,正方形ABCD的边长为2,A为坐标原点,AB和AD分别在x轴、y轴上,点E是BC边的中点,过点A的直线y=kx交线段DC于点F,连接EF,若AF平分∠DFE,则k的值为1或3.