题目内容
18.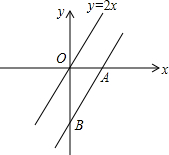 如图,把直线y=2x向下平移后得到直线AB,直线AB与x轴、y轴分别相交于点A、B.若△ABO的面积是1,则直线AB的解析式是( )
如图,把直线y=2x向下平移后得到直线AB,直线AB与x轴、y轴分别相交于点A、B.若△ABO的面积是1,则直线AB的解析式是( )| A. | y=3x+$\sqrt{2}$ | B. | y=2x-$\sqrt{2}$ | C. | y=3x-2 | D. | y=2x-2 |
分析 利用一次函数平移规律假设出直线AB的解析式,进而得出BO,AO的长,再利用三角形面积公式得出.
解答 解:设直线y=2x向下平移后得到直线AB的解析式为:y=2x+b,
则OB=-b,AO=-$\frac{b}{2}$,
故△ABO的面积是:$\frac{1}{2}$×(-b)×(-$\frac{b}{2}$)=1,
解得:b1=2(不合题意舍去),b2=-2,
则直线AB的解析式是:y=2x-2.
故选:D.
点评 此题主要考查了一次函数图象与几何变换,表示出AO,BO的长是解题关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
8.在多边形内角和公式的探究过程中,主要运用的数学思想是( )
| A. | 化归思想 | B. | 分类讨论 | C. | 方程思想 | D. | 数形结合思想 |
 如图,在△ABC中,AD是BC边上的中线,已知AB=7cm,AC=6cm,则△ABD和△ACD的周长差为1cm.
如图,在△ABC中,AD是BC边上的中线,已知AB=7cm,AC=6cm,则△ABD和△ACD的周长差为1cm.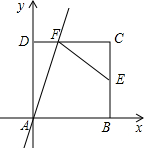 如图,正方形ABCD的边长为2,A为坐标原点,AB和AD分别在x轴、y轴上,点E是BC边的中点,过点A的直线y=kx交线段DC于点F,连接EF,若AF平分∠DFE,则k的值为1或3.
如图,正方形ABCD的边长为2,A为坐标原点,AB和AD分别在x轴、y轴上,点E是BC边的中点,过点A的直线y=kx交线段DC于点F,连接EF,若AF平分∠DFE,则k的值为1或3. 如图,在反比例函数$y=\frac{4}{x}$图象上有点A(a,1),过点A作y轴的平行线交某直线于点B,已知△AOB的面积是8,则直线OB的解析式为y=$\frac{5}{4}$x.
如图,在反比例函数$y=\frac{4}{x}$图象上有点A(a,1),过点A作y轴的平行线交某直线于点B,已知△AOB的面积是8,则直线OB的解析式为y=$\frac{5}{4}$x.