题目内容
15．
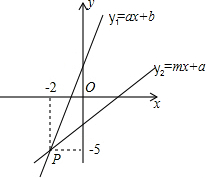如图，已知一次函数y1=ax+b（a≠0）和y2=mx+n（n≠0）的图象交于点P（-2，-5），则不等式ax+b＞mx+n的解集是（ ）| A． | x＞-5 | B． | x＞-2 | C． | x＜-2 | D． | x＜-5 |
分析 根据一次函数的图象和两函数的交点坐标即可得出答案．
解答 解：∵一次函数y1=ax+b（a≠0）和y2=mx+n（n≠0）的图象交于点P（-2，-5），
∴不等式ax+b＞mx+n的解集是x＞-2．
故选B．
点评 本题考查了一次函数与一元一次不等式的关系：从函数的角度看，就是寻求使一次函数y=ax+b的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线y=kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合．也考查了观察函数图象的能力．
练习册系列答案
科学实验活动册系列答案
相关题目
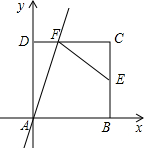如图，正方形ABCD的边长为2，A为坐标原点，AB和AD分别在x轴、y轴上，点E是BC边的中点，过点A的直线y=kx交线段DC于点F，连接EF，若AF平分∠DFE，则k的值为1或3．
如图，在反比例函数$y=\frac{4}{x}$图象上有点A（a，1），过点A作y轴的平行线交某直线于点B，已知△AOB的面积是8，则直线OB的解析式为y=$\frac{5}{4}$x．
4．给出下列函数：①y=2x-1；②y=$\frac{1}{x}$；③y=-2x2．从中任取一个函数，取出的函数符合条件“当x＞1时，函数值y随x增大而减小”的概率是（ ）
| A． | 1 | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | 0 |