题目内容
8.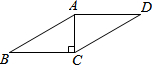 如图,在?ABCD中,过A点作高,垂足刚好为点C,AC=2,∠B=30°,则?ABCD的周长是( )
如图,在?ABCD中,过A点作高,垂足刚好为点C,AC=2,∠B=30°,则?ABCD的周长是( )| A. | $8+4\sqrt{3}$ | B. | $4+2\sqrt{3}$ | C. | 8 | D. | 4 |
分析 由AC⊥AD,∠B=30°,AC=2,根据含30°角的直角三角形的性质,可求得AB的长,然后由勾股定理求得BC的长,继而求得答案.
解答 解:∵AC⊥AD,∠B=30°,AC=2,
∴AB=2AC=4,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=2$\sqrt{3}$,
∴?ABCD的周长是:2(AB+BC)=8+4$\sqrt{3}$.
故选A.
点评 此题考查了平行四边形的性质、含30°角的直角三角形的性质以及勾股定理.注意平行四边形的对边相等是解题关键.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
18.甲型H7N9流感典型性病毒的直径约为0.00000156米,则此数用科学记数法可表示为( )
| A. | 15.6×10-5 | B. | 1.56×10-5 | C. | 1.56×10-6 | D. | 0.156×10-8 |
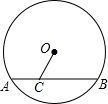 如图,已知AB是⊙O的弦,点C在线段AB上,OC=AC=4,CB=8.
如图,已知AB是⊙O的弦,点C在线段AB上,OC=AC=4,CB=8.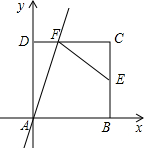 如图,正方形ABCD的边长为2,A为坐标原点,AB和AD分别在x轴、y轴上,点E是BC边的中点,过点A的直线y=kx交线段DC于点F,连接EF,若AF平分∠DFE,则k的值为1或3.
如图,正方形ABCD的边长为2,A为坐标原点,AB和AD分别在x轴、y轴上,点E是BC边的中点,过点A的直线y=kx交线段DC于点F,连接EF,若AF平分∠DFE,则k的值为1或3. 如图,抛物线y=ax2+bx+4与坐标轴交于A、B、C三点,直线y=$\frac{4}{3}$x+4与坐标轴交于B、C点,其中点A(4,0).
如图,抛物线y=ax2+bx+4与坐标轴交于A、B、C三点,直线y=$\frac{4}{3}$x+4与坐标轴交于B、C点,其中点A(4,0).