题目内容
12.如果菱形的两条对角线的长为a和b,且a、b满足(a-3)2+$\sqrt{b-4}$=0.那么菱形的面积等于6.分析 由a,b满足(a-3)2+$\sqrt{b-4}$=0,可求得a与b的值,然后由菱形的两条对角线的长为a和b,根据菱形的面积等于对角线积的一半,即可求得答案.
解答 解:∵a,b满足(a-5)2+$\sqrt{b-4}$=0,
∴a-3=0,b-4=0,
∴a=3,b=4,
∵菱形的两条对角线的长为a和b,
∴菱形的面积等于:$\frac{1}{2}$ab=6.
故答案为:6.
点评 本题考查了非负数的性质,菱形的性质,解题的根据是熟记菱形的面积等于对角线乘积的一半.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
4.给出下列函数:①y=2x-1;②y=$\frac{1}{x}$;③y=-2x2.从中任取一个函数,取出的函数符合条件“当x>1时,函数值y随x增大而减小”的概率是( )
| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 0 |
1.$\sqrt{x+1}$在实数范围内有意义,则x应满足的条件是( )
| A. | x>1 | B. | x≥1 | C. | x>-1 | D. | x≥-1 |
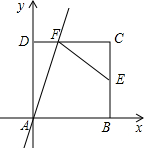 如图,正方形ABCD的边长为2,A为坐标原点,AB和AD分别在x轴、y轴上,点E是BC边的中点,过点A的直线y=kx交线段DC于点F,连接EF,若AF平分∠DFE,则k的值为1或3.
如图,正方形ABCD的边长为2,A为坐标原点,AB和AD分别在x轴、y轴上,点E是BC边的中点,过点A的直线y=kx交线段DC于点F,连接EF,若AF平分∠DFE,则k的值为1或3.