题目内容
8.如图,菱形ABCD中,E是AD的中点,将△CDE沿CE折叠后,点A和点D恰好重合,若菱形ABCD的面积为4$\sqrt{3}$,则菱形ABCD的周长是( )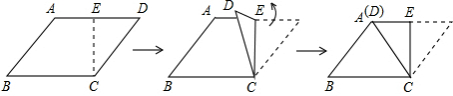
| A. | 8$\sqrt{2}$ | B. | 16$\sqrt{2}$ | C. | 8$\sqrt{3}$ | D. | 16$\sqrt{3}$ |
分析 先证明△ADC是等边三角形,根据锐角三角函数得出CE=$\frac{\sqrt{3}}{2}$CD,由菱形的面积求出CD,即可得出周长.
解答 解:∵四边形ABCD是菱形,
∴AD=CD,
又∵CD=AC,
∴AD=CD=AC,
即△ADC是等边三角形,
∴∠D=60°,
∴CE=CD•sin60°=$\frac{\sqrt{3}}{2}$CD,
∵菱形ABCDABCD的面积=AD•CE=$\frac{\sqrt{3}}{2}$CD2=4$\sqrt{3}$,
∴CD=2$\sqrt{2}$,
∴菱形ABCD的周长为2$\sqrt{2}$×4=8$\sqrt{2}$;
故选:A.
点评 本题考查了菱形的性质、翻折变换以及锐角三角函数的运用;证明△ADC是等边三角形,根据面积求出边长是解决问题的关键.

练习册系列答案
相关题目
16.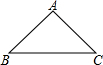 如图,已知△ABC中,AB=AC=5,BC=8.则cosB的值是( )
如图,已知△ABC中,AB=AC=5,BC=8.则cosB的值是( )
 如图,已知△ABC中,AB=AC=5,BC=8.则cosB的值是( )
如图,已知△ABC中,AB=AC=5,BC=8.则cosB的值是( )| A. | 1.25 | B. | 0.8 | C. | 0.6 | D. | 0.625 |
 如图,BE、CF都是△ABC的角平分线,且∠BDC=110°,则∠A=40°.
如图,BE、CF都是△ABC的角平分线,且∠BDC=110°,则∠A=40°. 如图,已知AD∥BC,AB⊥AD,点E,F分别在射线AD,BC上.已知点E与点B关于AC对称,点E与点F关于BD对称.
如图,已知AD∥BC,AB⊥AD,点E,F分别在射线AD,BC上.已知点E与点B关于AC对称,点E与点F关于BD对称.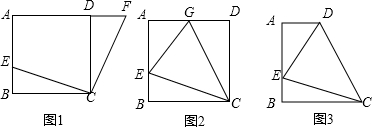
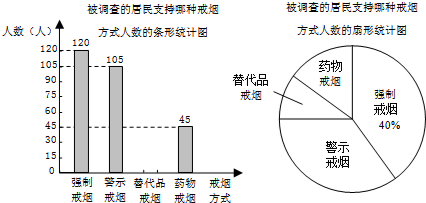
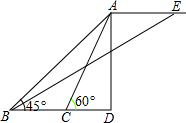 如图,广场上空有一个气球A,地面上点B、C、D在一条直线上,BC=20m,两个观测者在点B、C两处分别测得气球A的仰角∠ABD=45°,∠ACD=60°,当气球沿与BC的平行的路线飘移10秒后至达点E,在B处测得气球的仰角为30°.
如图,广场上空有一个气球A,地面上点B、C、D在一条直线上,BC=20m,两个观测者在点B、C两处分别测得气球A的仰角∠ABD=45°,∠ACD=60°,当气球沿与BC的平行的路线飘移10秒后至达点E,在B处测得气球的仰角为30°.