题目内容
17.已知直线y=kx+b经过点(k,3)和(1,k),则k的值为( )| A. | $\sqrt{3}$ | B. | ±$\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $±\sqrt{2}$ |
分析 由两点均在直线上可得出关于k、b的二元二次方程组,解方程组即可得出结论.
解答 解:由已知得:$\left\{\begin{array}{l}{3={k}^{2}+b}\\{k=k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\sqrt{3}}\\{b=0}\end{array}\right.$或$\left\{\begin{array}{l}{k=-\sqrt{3}}\\{b=0}\end{array}\right.$.
故选B.
点评 本题考查了一次函数图象上点的坐标特征以及解二元二次方程组,解题的关键是结合题意得出关于k、b的二元二次方程组.本题属于基础题,难度不大,解决该题型题目时,根据点在直线上得出方程(或方程组)是关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
12.不等式组$\left\{\begin{array}{l}x>0\\ x<1\end{array}\right.$的解集是( )
| A. | 0<x<1 | B. | x>0 | C. | x<1 | D. | 无解 |
2.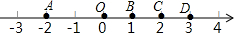 如图,已知数轴上的点A,O,B,C,D分别表示数-2,0,1,2,3,则表示数2-$\sqrt{2}$的点P应落在线段( )
如图,已知数轴上的点A,O,B,C,D分别表示数-2,0,1,2,3,则表示数2-$\sqrt{2}$的点P应落在线段( )
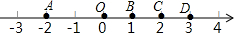 如图,已知数轴上的点A,O,B,C,D分别表示数-2,0,1,2,3,则表示数2-$\sqrt{2}$的点P应落在线段( )
如图,已知数轴上的点A,O,B,C,D分别表示数-2,0,1,2,3,则表示数2-$\sqrt{2}$的点P应落在线段( )| A. | AO上 | B. | OB上 | C. | BC上 | D. | CD上 |
9.把方程x2+4x+1=0配方成(x+p)2+q=0的形式后,p2+q2的值是( )
| A. | 41 | B. | 14 | C. | 13 | D. | 7 |
4.下列根式中是最简二次根式的是( )
| A. | $\sqrt{{a}^{2}+1}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{8}$ | D. | $\sqrt{0.1}$ |

 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,-2),B(3,-1),C(1,-1).
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,-2),B(3,-1),C(1,-1).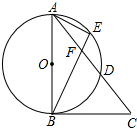 如图,在△ABC中,以AB为直径的⊙O与边AC交于点D,E为$\widehat{AD}$上的一点,BE交AC于点F,CF=BC,∠EAF=∠EBA.
如图,在△ABC中,以AB为直径的⊙O与边AC交于点D,E为$\widehat{AD}$上的一点,BE交AC于点F,CF=BC,∠EAF=∠EBA.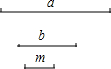 如图所示,已知线段a,b,m,
如图所示,已知线段a,b,m,