题目内容
7.如图,在正方形ABCD中,点E在边AB上,点F在AB的延长线上,点G在边AD上,EF=nAB,DG=nAE,连接DE,FG相交于点H.(1)若n=1,如图1,求∠EHF的度数;
(2)若n=$\frac{1}{2}$,如图2,求tan∠EHF的值.

分析 (1)连接FC和CG(如图1),先证明△AED≌△DGC,同理△FBC≌△EAD,再证明△GFC是等腰直角三角形即可.
(2)如图2,过点F作FM∥ED交CD于M,连接GM,先证明△DGM∽△AED,得∠ADE=∠DMG,$\frac{GM}{DB}$=$\frac{DG}{AE}$=$\frac{1}{2}$,再证明△FMG是直角三角形即可.
解答 解:(1)连接FC和CG(如图1),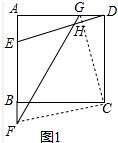 ∵四边形ABCD为正方形,AE=BF=GD,
∵四边形ABCD为正方形,AE=BF=GD,
∴AB=BC=DC=AD,∠A=∠ABC=∠FBC=∠CDG=90°,
在△EAD和△GDC中,
$\left\{\begin{array}{l}{AE=DG}\\{∠A=∠GDC}\\{AD=DC}\end{array}\right.$,
∴△AED≌△DGC(SAS),
同理△FBC≌△EAD.
∴CF=GC,∠AED=∠BFC,∠BCF=∠DCG,
∴ED∥FC,
∴∠EHF=∠GFC,
又∵∠BCD=90°=∠BCG+∠GCD=∠BCG+∠BCF=∠GCF,
∴△GCF是等腰直角三角形,
∴∠GFC=∠FGC=45°,
∴∠EHF=45°;(4分)
(2)如图2,过点F作FM∥ED交CD于M,连接GM.
∵正方形ABCD中,AB∥CD,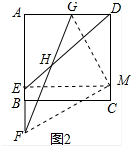
∴四边形EFMD为平行四边形.
∴EF=DM,DE=FM.
∴∠3=∠4,∠EHF=∠HFM=α.
∵EF=$\frac{1}{2}$CD,GD=$\frac{1}{2}$AE,
∴$\frac{GD}{AE}=\frac{DM}{AD}$.
∵∠A=∠GDM=90°,
∴△DGM∽△AED.
∴∠ADE=∠DMG,$\frac{GM}{DB}$=$\frac{DG}{AE}$=$\frac{1}{2}$
∵∠DMG+∠MGD=90°,
∴∠ADE+∠DGM=90°,
∴GM⊥DE,∵ED∥FM,
∴GM⊥FM,∠EHF=∠GFM,
∴tan∠GFM=$\frac{GM}{FM}$=$\frac{GM}{DE}$=$\frac{1}{2}$.
点评 本题考查正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质、三角函数等知识,解题的关键是添加辅助线,构造全等三角形,属于中考常考题型.

| A. | 0.2,$\sqrt{3}$ | B. | $\frac{{\sqrt{2}}}{3}$,3 | C. | $3\sqrt{2}$,π | D. | $\sqrt{4}$,1 |
| A. | ∠A=60°,∠D=120° | B. | ∠A=120°,∠D=60° | C. | ∠A=60°,∠D=60° | D. | ∠A=120°,∠D=120° |
| A. | ($\frac{1}{3}$)-1=3 | B. | (-2)3=8 | C. | (a-b)2=a2-b2 | D. | (a2)3÷a3=a2 |
| A. | 2x•3x2=6x2 | B. | (-3a2b)2=6a4b2 | C. | -a2+2a2=a2 | D. | (a+b)(a-2b)=a2-2b2 |
| A. | 这组数据的平均数是169 | B. | 这组数据的众数是170 | ||
| C. | 这组数据的中位数是169 | D. | 这组数据的方差是66 |
| A. | $\sqrt{3}$ | B. | ±$\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $±\sqrt{2}$ |




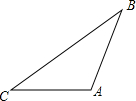 实践与操作:如图,在△ABC中,AB=3,∠C=30°.
实践与操作:如图,在△ABC中,AB=3,∠C=30°.