题目内容
8. 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,-2),B(3,-1),C(1,-1).
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,-2),B(3,-1),C(1,-1).(1)将△ABC向左平移3个单位得到△A1B1C1,在坐标系中画出△A1B1C1,并写出点A的对应点A1的坐标;
(2)画出△ABC绕原点O逆时针旋转90°后得到的△A2B2C2,并写出A的对应点A2的坐标;
(3)求(2)中点A所走过的路线长.
分析 (1)利用点平移的坐标规律,写出点A、B、C平移后的对应点A1、B1、C1的坐标,然后描点即可得到△A1B1C1;
(2)利用网格特点和旋转的性质,画出点A、B、C旋转后的对应点A2、B2、C2,则△A2B2C2为所作;
(3)根据弧长公式列式计算即可求解.
解答 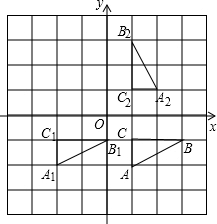 解:(1)如图,△A1B1C1为所求,点A1的坐标(-2,-2);
解:(1)如图,△A1B1C1为所求,点A1的坐标(-2,-2);
(2)如图,△A2B2C2为所求;
(3)OA=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
点A所走过的路线长为$\frac{90π×\sqrt{5}}{180}$=$\frac{\sqrt{5}π}{2}$.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了平移变换和弧长公式.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
19.下列各式计算正确的是( )
| A. | 2x•3x2=6x2 | B. | (-3a2b)2=6a4b2 | C. | -a2+2a2=a2 | D. | (a+b)(a-2b)=a2-2b2 |
16.某中学九年级舞蹈兴趣小组8名学生的身高分别为(单位:cm):168,165,168,166,170,170,175,170,则下列说法错误的是( )
| A. | 这组数据的平均数是169 | B. | 这组数据的众数是170 | ||
| C. | 这组数据的中位数是169 | D. | 这组数据的方差是66 |
3.对于近似数0.7048,下列说法中正确的是( )
| A. | 它的准确值x的范围是0.70475<x<0.70485 | |
| B. | 它有三个有效数字 | |
| C. | 对它四舍五入精确到百分位为0.71 | |
| D. | 用科学记数法表示它为7.048×10-1 |
17.已知直线y=kx+b经过点(k,3)和(1,k),则k的值为( )
| A. | $\sqrt{3}$ | B. | ±$\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $±\sqrt{2}$ |




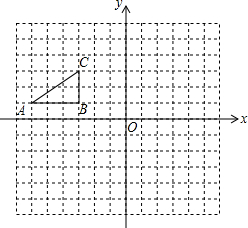 如图所示,方格纸中的每个小方格都是边长为1的正方形,Rt△ABC的项点均在格点上.A(-6,1)B(-3,1)C(-3,3)
如图所示,方格纸中的每个小方格都是边长为1的正方形,Rt△ABC的项点均在格点上.A(-6,1)B(-3,1)C(-3,3)