题目内容
5.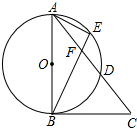 如图,在△ABC中,以AB为直径的⊙O与边AC交于点D,E为$\widehat{AD}$上的一点,BE交AC于点F,CF=BC,∠EAF=∠EBA.
如图,在△ABC中,以AB为直径的⊙O与边AC交于点D,E为$\widehat{AD}$上的一点,BE交AC于点F,CF=BC,∠EAF=∠EBA.(1)判断BC与⊙O的位置关系,并说明理由;
(2)若AB=2$\sqrt{5}$,AC=6,求BE的长.
分析 (1)BC是⊙O切线,只要证明∠ABC=90°即可.
(2)利用△AEB∽△FDB,得$\frac{EB}{BD}$=$\frac{AB}{BF}$,只要求出BD、BF即可解决问题.
解答 解:(1)BC与⊙O相切.理由如下:
∵AB为直径,
∴∠E=90°,
∴∠1+∠5=90°,
∵∠4=∠5,∠1=∠2,
∴∠4+∠2=90°,
∵CB=CF,
∴∠4=∠CBF,
∴∠CBF+∠2=90°,
∴AB⊥BC,
∴BC为⊙O的切线;
(2)连接BD则BD⊥AC,
在RT△ABC中,∠ABC=90°,AB=2$\sqrt{5}$,AC=6,
∴BC=CF=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{{6}^{2}-(2\sqrt{5})^{2}}$=4,
∵$\frac{1}{2}$•AC•BD=$\frac{1}{2}$•BC•AB,
∴BD=$\frac{AB•BC}{AC}$=$\frac{4\sqrt{5}}{3}$,
∴CD=$\sqrt{B{C}^{2}-B{D}^{2}}$=$\frac{8}{3}$,DF=4-$\frac{8}{3}$=$\frac{4}{3}$,
∴BF=$\sqrt{B{D}^{2}+D{F}^{2}}$=$\frac{4\sqrt{6}}{3}$,
∵∠2=∠3,∠AEB=∠BDF,
∴△AEB∽△FDB,
∴$\frac{EB}{BD}$=$\frac{AB}{BF}$,
∴$\frac{BE}{\frac{4\sqrt{5}}{3}}$=$\frac{2\sqrt{5}}{\frac{4\sqrt{6}}{3}}$,
∴BE=$\frac{5\sqrt{6}}{3}$.
点评 本题考查直线与圆的位置关系、相似三角形的判定和性质、切线的判定、勾股定理等知识,解题的关键是寻找相似三角形解决问题,属于中考常考题型.

 高中必刷题系列答案
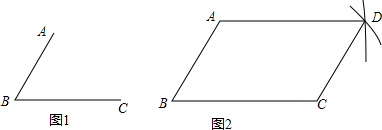
高中必刷题系列答案| A. | ∠A=60°,∠D=120° | B. | ∠A=120°,∠D=60° | C. | ∠A=60°,∠D=60° | D. | ∠A=120°,∠D=120° |
| A. | 这组数据的平均数是169 | B. | 这组数据的众数是170 | ||
| C. | 这组数据的中位数是169 | D. | 这组数据的方差是66 |
| A. | 3:2 | B. | 3:5 | C. | 2:3 | D. | 2:5 |
| A. | $\sqrt{3}$ | B. | ±$\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $±\sqrt{2}$ |
| A. | $\left\{\begin{array}{l}{2x-5y=8}\\{x+y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=1}\\{x=\frac{1}{y}+3}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x-3y=2}\\{2x+y=5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{1}{2}x+\frac{1}{3}y=2}\\{\frac{1}{3}x-\frac{1}{2}y=3}\end{array}\right.$ |
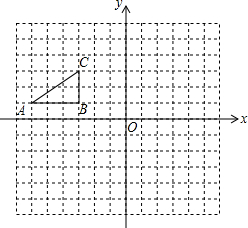 如图所示,方格纸中的每个小方格都是边长为1的正方形,Rt△ABC的项点均在格点上.A(-6,1)B(-3,1)C(-3,3)
如图所示,方格纸中的每个小方格都是边长为1的正方形,Rt△ABC的项点均在格点上.A(-6,1)B(-3,1)C(-3,3)