题目内容
12.解方程.(1)5x(x-3)=6-2x;
(2)$\frac{2x}{x+3}+1=\frac{7}{2x+6}$;.
分析 (1)移项,再分解因式,即可得出两个一元一次方程,求出方程的解即可;
(2)先去分母,化为一元一次方程,求得方程的解,进一步检验得出答案即可.
解答 解:(1)5x(x-3)=6-2x,
5x(x-3)+2(x-3)=0,
(x-3)(5x+2)=0,
x-3=0,5x+2=0,
解得:x1=3,x2=-$\frac{2}{5}$;
(2)$\frac{2x}{x+3}+1=\frac{7}{2x+6}$
4x+2x+6=7
解得:x=$\frac{1}{6}$,
检验:当x=$\frac{1}{6}$时,2x+6≠0
所以x=$\frac{1}{6}$是原分式方程的解.
点评 本题考查了解一元二次方程与分式方程,关键是能把一元二次方程和分式方程转化成一元一次方程,进而求得方程的解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下列计算中错误的是( )
| A. | (x2-5)(3x-7)=6x2-29x+35 | B. | (3x+7)(10x-8)=30x2-46x-56 | ||
| C. | (-3x+$\frac{1}{2}$)(-$\frac{1}{3}x$)=x${\;}^{2}-\frac{1}{6}$x | D. | (1-x)(x+1)+(x+2)(x-2)=-3 |
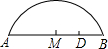 如图,一拱桥呈抛物线状,桥的最大高度是32m,跨度是80m,在线段AB上距离中心M20m的D处,桥的高度是24m.
如图,一拱桥呈抛物线状,桥的最大高度是32m,跨度是80m,在线段AB上距离中心M20m的D处,桥的高度是24m. 如图,在直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴,y轴分别交于A,B两点,以AB为边在第二象限内作矩形ABCD,使AD=$\sqrt{5}$.
如图,在直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴,y轴分别交于A,B两点,以AB为边在第二象限内作矩形ABCD,使AD=$\sqrt{5}$. 如图,直线a∥b∥c,若$\frac{AC}{CE}$=$\frac{2}{3}$,BD=3,则DF的长为4.5.
如图,直线a∥b∥c,若$\frac{AC}{CE}$=$\frac{2}{3}$,BD=3,则DF的长为4.5. 如图,AB⊥BD,EF⊥BD,CD⊥BD,且AB:EF:CD=3:5:8 求AE:EC的值.
如图,AB⊥BD,EF⊥BD,CD⊥BD,且AB:EF:CD=3:5:8 求AE:EC的值.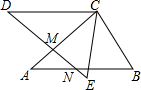 如图,AB=DE,AC=DC,BC=EC,DE与AC、AB分别交于点M、N,CE与AB交于点H,且∠A=∠BCE=40°,∠B=60°
如图,AB=DE,AC=DC,BC=EC,DE与AC、AB分别交于点M、N,CE与AB交于点H,且∠A=∠BCE=40°,∠B=60°