题目内容
2.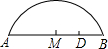 如图,一拱桥呈抛物线状,桥的最大高度是32m,跨度是80m,在线段AB上距离中心M20m的D处,桥的高度是24m.
如图,一拱桥呈抛物线状,桥的最大高度是32m,跨度是80m,在线段AB上距离中心M20m的D处,桥的高度是24m.
分析 根据题意假设解析式为y=ax2+bx+c,用待定系数法求出解析式.然后把自变量的值代入求解对应函数值即可.
解答 解:设抛物线的方程为y=ax2+bx+c
已知抛物线经过(0,32),(-40,0),(40,0),
可得$\left\{\begin{array}{l}{c=32}\\{0=1600a-40b+c}\\{0=1600a+40b+c}\end{array}\right.$,
可得a=-$\frac{1}{50}$,b=0,c=32,
故解析式为y=-$\frac{1}{50}$x2+32,
当x=20时,y=24.
故答案为:24.
点评 本题考查点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.x10不可能写出如下式子( )
| A. | x2•x4•(x2)2 | B. | (x3)3•x | C. | (-x)3•(-x)5•(-x)2 | D. | (x5)5 |
 已知实数a,b,c在数轴上所对应的点如图所示,完成下列各题.
已知实数a,b,c在数轴上所对应的点如图所示,完成下列各题. 如图,木匠小王想从对角线长为80cm的正方形木板上截下一个最大的洞,试求这个圆的直径是多少?
如图,木匠小王想从对角线长为80cm的正方形木板上截下一个最大的洞,试求这个圆的直径是多少? 已知:如图,AE是△ABC外角的平分线,且AE∥BC.
已知:如图,AE是△ABC外角的平分线,且AE∥BC.