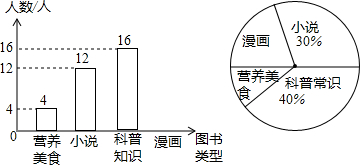
题目内容
1.一次函数y=kx+b,当-1≤x≤1时,相应的函数值是0≤y≤3.试求k、b的值.分析 根据一次函数的增减性,可知本题分两种情况:
①当k>0时,y随x的增大而增大,把x=-1,y=0;x=1,y=3代入一次函数的解析式y=kx+b(k≠0),运用待定系数法即可求解;
②当k<0时,y随x的增大而减小,把x=-1,y=3;x=1,y=0代入一次函数的解析式y=kx+b(k≠0),运用待定系数法即可求解.
解答 解:分两种情况:
①当k>0时,把x=-1,y=0;x=1,y=3代入一次函数的解析式y=kx+b(k≠0),
得$\left\{\begin{array}{l}{-k+b=0}\\{k+b=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{3}{2}}\\{b=\frac{3}{2}}\end{array}\right.$,
则这个函数的解析式是y=$\frac{3}{2}$x+$\frac{3}{2}$;
②当k<0时,把x=-1,y=3;x=1,y=0代入一次函数的解析式y=kx+b(k≠0),
得$\left\{\begin{array}{l}{-k+b=3}\\{k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{3}{2}}\\{b=\frac{3}{2}}\end{array}\right.$,
则这个函数的解析式是y=-$\frac{3}{2}$x+$\frac{3}{2}$;
综上可得,k=$\frac{3}{2}$,b=$\frac{3}{2}$或k=-$\frac{3}{2}$,b=$\frac{3}{2}$.
点评 本题主要考查一次函数的性质,当k>0时,y随x的增大而增大,当k<0时,y随x的增大而减小,注意要分情况讨论.

 名校课堂系列答案
名校课堂系列答案| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 没有实数根 | D. | 不能确定 |
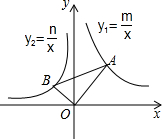 如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数y1=$\frac{m}{x}$的图象经过点A,反比例函数y2=$\frac{n}{x}$的图象经过点B,则下列关于m,n的关系正确的是( )
如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数y1=$\frac{m}{x}$的图象经过点A,反比例函数y2=$\frac{n}{x}$的图象经过点B,则下列关于m,n的关系正确的是( )| A. | m=$\frac{\sqrt{3}}{3}$n | B. | m=-$\sqrt{3}$n | C. | m=-$\frac{\sqrt{3}}{3}$n | D. | m=-3n |
| x | 6.17 | 6.18 | 6.19 | 6.20 |
| y=ax2+bx+c | -0.03 | -0.01 | 0.02 | 0.06 |
| A. | -0.01-0.02之间 | B. | 0.02-0.06之间 | C. | 6.17-6.18之间 | D. | 6.18-6.19之间 |
| A. | 4×103千米 | B. | 6×103千米 | C. | 8×103千米 | D. | 6×104千米 |
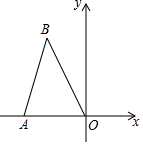 如图,在△ABO中,BA=BO=4,OA=2.则B的坐标是(-1,$\sqrt{15}$).
如图,在△ABO中,BA=BO=4,OA=2.则B的坐标是(-1,$\sqrt{15}$).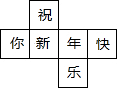 如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面,与“快”相对的面上的汉字是新.
如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面,与“快”相对的面上的汉字是新.