题目内容
8.已知△BAC和△BDE都是等腰直角三角形,∠BAC=∠BDE=90°.(1)如图1,点E、B、C三点在一条直钱上,连接AE,若∠AEC=30°,BC=4,求BE的长.
(2)如图2,将△BDE以点B为旋转中心顺时针旋转,当C在ED延长线上时,EC交AB于点H.求证:∠BAE=2∠BCH.

分析 (1)如图1中,作AH⊥BC于H.利用等腰直角三角形的性质求出AH,在Rt△AEH中,根据EH=$\frac{AH}{tan30°}$,求出EH即可解决问题.
(2)如图2中,连接AD.由△BHD∽△CHA,推出△AHD∽△CHB,推出∠ADH=∠CBH=45°,∠DAH=∠BCH,推出∠ADB=90°+45°=135°,推出∠ADE=360°-90°-135°=135°,即∠ADE=∠ADB,推出△ADE≌△ADB,即可解决问题.
解答 (1)解:如图1中,作AH⊥BC于H.
∵AB=AC,∠BAC=90°,AH⊥BC,
∴AH=BH=HC=2,
在Rt△AEH中,∵∠AHE=90°,AH=2,∠AEH=30°,
∴EH=$\frac{AH}{tan30°}$=2$\sqrt{3}$,
∴BE=EH-BH=2$\sqrt{3}$-2.
(2)证明:如图2中,连接AD.
∵∠BDH=∠HAC,∠BHD=∠CHA,
∴△BHD∽△CHA,
∴$\frac{DH}{AH}$=$\frac{BH}{CH}$,
∴$\frac{DH}{BH}$=$\frac{AH}{CH}$,∵∠AHD=∠CHB,
∴△AHD∽△CHB,
∴∠ADH=∠CBH=45°,∠DAH=∠BCH,
∴∠ADB=90°+45°=135°,
∴∠ADE=360°-90°-135°=135°,
∴∠ADE=∠ADB,
在△ADE和△ADB中,$\left\{\begin{array}{l}{AD=AD}\\{∠ADE=∠ADB}\\{DE=DB}\end{array}\right.$,
∴△ADE≌△ADB,
∴∠DAE=∠DAB,
∵∠DAB=∠BCH,
∴∠BAE=2∠BCH.
点评 本题考查等腰直角三角形的性质、全等三角形的判定和性质、相似三角形的判定和性质、旋转变换、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

| A. | (1+40%)×30%x | B. | (1+40%)(1-30%)x | C. | $\frac{x}{(1+40%)×30%}$ | D. | $\frac{x}{(1+40%)(1-30%)}$ |
| A. | a≥-5 | B. | a<1 | ||
| C. | -1<a<-2+$\frac{3\sqrt{5}}{2}$ | D. | -2-$\frac{3\sqrt{5}}{2}$<a<-5或1<a<-2+$\frac{3\sqrt{5}}{2}$ |
| A. | (-2,3) | B. | (2,3) | C. | (3,-2) | D. | (3,2) |
| A. | $\frac{720}{48+x}$-$\frac{720}{x}$=5 | B. | $\frac{720}{48}$+5=$\frac{720}{48+x}$ | C. | $\frac{720}{48}$-$\frac{720}{x}$=5 | D. | $\frac{720}{48}$-$\frac{720}{48+x}$=5 |
| A. | 2 | B. | 3 | C. | 6 | D. | 4 |
 如图,在Rt△ABC中,∠ACB=90°,AC=BC,点M在AC边上,且AM=1,MC=4,动点P在AB边上,连接PC,PM,则PC+PM的最小值是( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC,点M在AC边上,且AM=1,MC=4,动点P在AB边上,连接PC,PM,则PC+PM的最小值是( )| A. | $\sqrt{17}$ | B. | 6 | C. | $\sqrt{26}$ | D. | 7 |
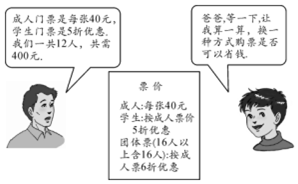 在“五一”期间,小明、小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
在“五一”期间,小明、小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题: