题目内容
19.如果函数y=(a-1)x2+3x+a+5的图象经过平面直角坐标系的三个象限,那么a的取值范围是( )| A. | a≥-5 | B. | a<1 | ||
| C. | -1<a<-2+$\frac{3\sqrt{5}}{2}$ | D. | -2-$\frac{3\sqrt{5}}{2}$<a<-5或1<a<-2+$\frac{3\sqrt{5}}{2}$ |
分析 由抛物线与x轴有两个不同的交点结合根的判别式,即可得出a的取值范围,再分抛物线的开口方向不同,即可得出关于a的一元一次不等式,解之结合a的取值范围,即可得出结论.
解答 解:当关于x的一元二次方程(a-1)x2+3x+a+5=0有两个不相等的实数根时,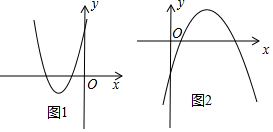
△=32-4(a-1)(a+5)=-4a2-16a+29>0,
解得:-2-$\frac{3\sqrt{5}}{2}$<a<-2+$\frac{3\sqrt{5}}{2}$.
函数y=(a-1)x2+3x+a+5的图象经过平面直角坐标系的三个象限分两种情况:
①抛物线开口向上时,如图1所示,此时a-1>0,
∴1<a<-2+$\frac{3\sqrt{5}}{2}$;
②抛物线开口向下时,如图2所示,此时a+5<0,
解得:-2-$\frac{3\sqrt{5}}{2}$<a<-5.
故选D.
点评 本题考查二次函数的图象与性质、二次函数与x轴的交点、二次函数与y轴交点等知识点,解题关键是确定“函数图象经过三个象限”所满足的条件.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
9.如果一个多边形的内角和等于它的外角和的2倍,则这个多边形是( )
| A. | 三角形 | B. | 四边形 | C. | 五边形 | D. | 六边形 |
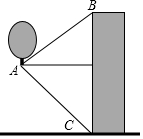 热气球的探测器显示,从热气球底部A处看一栋高楼顶部B的仰角为30°,看这栋楼底部C的俯角为45°,已知楼高是120m,热气球若要飞越高楼,问至少要继续上升多少米?(结果保留根号)
热气球的探测器显示,从热气球底部A处看一栋高楼顶部B的仰角为30°,看这栋楼底部C的俯角为45°,已知楼高是120m,热气球若要飞越高楼,问至少要继续上升多少米?(结果保留根号)
 如图,AB是半圆O的直径,点C在半圆O上,AB=4cm,∠CAB=60°,P是弧$\widehat{BC}$上的一个动点,连接AP,过C点作CD⊥AP于D,连接BD,在点P移动的过程中,BD的最小值是($\sqrt{13}$-1)cm.
如图,AB是半圆O的直径,点C在半圆O上,AB=4cm,∠CAB=60°,P是弧$\widehat{BC}$上的一个动点,连接AP,过C点作CD⊥AP于D,连接BD,在点P移动的过程中,BD的最小值是($\sqrt{13}$-1)cm.