��Ŀ����
3��С����ѧϰ���θ�ʽ����һЩ�����ŵ�ʽ�ӿ���д����һ��ʽ�ӵ�ƽ�����磺3+2$\sqrt{2}$=��1+$\sqrt{2}$��2������˼����С������������̽������a+b$\sqrt{2}$=��m+n$\sqrt{2}$��2������a��b��m��n��Ϊ������������a+b$\sqrt{2}$=m2+2n2+2mn$\sqrt{2}$����a=m2+2n2��b=2mn������С�����ҵ���һ�ְѲ���a+b$\sqrt{2}$��ʽ�ӻ�Ϊƽ��ʽ�ķ�����
���ҷ���С���ķ���̽��������������⣺
��1����a��b��m��n��Ϊ������ʱ����a+b$\sqrt{3}$=��m+n$\sqrt{3}$��2���ú�m��n��ʽ�ӷֱ��ʾa��b����a=m2+3n2��b=2mn��
��2����a+4$\sqrt{3}$=��m+n$\sqrt{3}$��2����a��m��n��Ϊ����������a��ֵ��
���� ��1��ֱ��������ȫƽ����ʽ��ԭʽ���ν����ó��𰸣�
��2��ֱ��������ȫƽ����ʽ��ԭʽ���εó�m��n��ֵ�������ó��𰸣�
��� �⣺��1����a+b$\sqrt{3}$=��m+n$\sqrt{3}$��2��
��a+b$\sqrt{3}$=m2+3n2+2$\sqrt{3}$mn��
��a=m2+3n2��b=2mn��
�ʴ�Ϊ��m2+3n2��2mn��
��2�������⣬��$\left\{\begin{array}{l}{a={m}^{2}+3{n}^{2}}\\{4=2mn}\end{array}\right.$��
��4=2mn����m��n��������
��m=2��n=1��m=1��n=2��
��a=22+3��12=7��a=12+3��22=13��
���� ������Ҫ�����˶��θ�ʽ�Ļ�������Լ���ȫƽ����ʽ����ȷӦ����ȫƽ����ʽ�ǽ���ؼ���

��ϰ��ϵ�д�
 ����ͬѧһ����ʦȫ�źþ�ϵ�д�
����ͬѧһ����ʦȫ�źþ�ϵ�д�
�����Ŀ
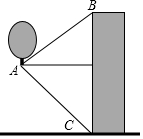 �������̽������ʾ����������ײ�A����һ����¥����B������Ϊ30�㣬���ⶰ¥�ײ�C�ĸ���Ϊ45�㣬��֪¥����120m����������Ҫ��Խ��¥��������Ҫ�������������ף�������������ţ�
�������̽������ʾ����������ײ�A����һ����¥����B������Ϊ30�㣬���ⶰ¥�ײ�C�ĸ���Ϊ45�㣬��֪¥����120m����������Ҫ��Խ��¥��������Ҫ�������������ף�������������ţ�
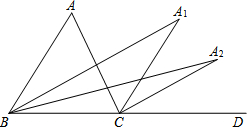 ��ͼ����ACD�ǡ�ABC����ǣ���1�β�������ABC��ƽ�������ACD��ƽ���߽��ڵ�A1����2�β�������A1BC��ƽ�������A1CD��ƽ���߽��ڵ�A2������n�β�������An-1BC��ƽ�������An-1CD��ƽ���߽��ڵ�An�����A2���A֮���������ϵ�ǡ�A2=$\frac{1}{4}$��A������A=64�㣬��An��4�㣬��n��ȡֵ��Χ��n��4��
��ͼ����ACD�ǡ�ABC����ǣ���1�β�������ABC��ƽ�������ACD��ƽ���߽��ڵ�A1����2�β�������A1BC��ƽ�������A1CD��ƽ���߽��ڵ�A2������n�β�������An-1BC��ƽ�������An-1CD��ƽ���߽��ڵ�An�����A2���A֮���������ϵ�ǡ�A2=$\frac{1}{4}$��A������A=64�㣬��An��4�㣬��n��ȡֵ��Χ��n��4�� ��ͼ��A��E��F��C��һ��ֱ���ϣ�AF=CE����E��F�ֱ���DE��AC��BF��AC������ֱ�ΪE��F��AB=CD����֤��BF=DE��
��ͼ��A��E��F��C��һ��ֱ���ϣ�AF=CE����E��F�ֱ���DE��AC��BF��AC������ֱ�ΪE��F��AB=CD����֤��BF=DE��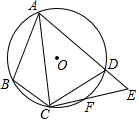 ��ͼ���ı���ABCD�ڽ��ڡ�O��F��$\widehat{CD}$��һ�㣬��$\widehat{DF}$=$\widehat{BC}$������CF���ӳ���AD���ӳ����ڵ�E������AC������ABC=105�㣬��BAC=30�㣬���E�Ķ���Ϊ��������
��ͼ���ı���ABCD�ڽ��ڡ�O��F��$\widehat{CD}$��һ�㣬��$\widehat{DF}$=$\widehat{BC}$������CF���ӳ���AD���ӳ����ڵ�E������AC������ABC=105�㣬��BAC=30�㣬���E�Ķ���Ϊ��������