题目内容
6. 如图,正方形ABCD中,P为CD上一动点,过C作CM⊥AP交AP于M并延长AP,使MN=AM,连BD交AN于E,连CN.
如图,正方形ABCD中,P为CD上一动点,过C作CM⊥AP交AP于M并延长AP,使MN=AM,连BD交AN于E,连CN.(1)求证:CN=BD;
(2)连BM、DM,试探究BM、DM与MN之间的数量关系.
分析 (1)如图1中,连接AC.由AM=MN,CM⊥AN,推出CN=CA,由四边形ABCD是正方形,推出BD=AC,延长即可证明.
(2)结论:MB+MD=$\sqrt{2}$MA.如图2中,连接AC交BD于O,延长DB到F使得BF=DM,连接OM.只要证明△ADM≌△ABF,推出AM=AF,∠DAM=∠BAF,推出∠MAF=∠DAB=90°,推出MF=$\sqrt{2}$MA,延长即可解决问题.
解答 (1)证明:如图1中,连接AC.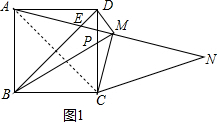
∵AM=MN,CM⊥AN,
∴CN=CA,
∵四边形ABCD是正方形,
∴BD=AC,
∴CN=BD.
(2)解:结论:MB+MD=$\sqrt{2}$MA.
理由:如图2中,连接AC交BD于O,延长DB到F使得BF=DM,连接OM.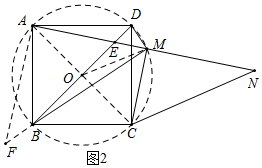
在Rt△AMC中,∵OA=OC,
∴OM=OA=OC=OB=DO,
∴A、B、C、M、D五点共圆,
∴∠ADM+∠ABD=180°,
∵∠ABD+∠ABF=180°,
∴∠ADM=∠ABF,∵AD=AB,DM=BF,
∴△ADM≌△ABF,
∴AM=AF,∠DAM=∠BAF,
∴∠MAF=∠DAB=90°,
∴MF=$\sqrt{2}$MA,
∵MF=BF+MB=MD+MB,
∴MB+MD=$\sqrt{2}$MA.
点评 本题考查全等三角形的判定和性质、正方形的性质、四点共圆、等腰直角三角形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
16.以下列各组数据为三角形的三边,能构成直角三角形的是( )
| A. | 4cm,8cm,7cm | B. | 2cm,2cm,2cm | C. | 2cm,2cm,4cm | D. | 6cm,8cm,10cm |
11. 一次函数y=kx+b的图象如图所示,当y<0时,x的取值范围是( )
一次函数y=kx+b的图象如图所示,当y<0时,x的取值范围是( )
 一次函数y=kx+b的图象如图所示,当y<0时,x的取值范围是( )
一次函数y=kx+b的图象如图所示,当y<0时,x的取值范围是( )| A. | x<-1 | B. | x>-1 | C. | x<2 | D. | x>2 |
 如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB、AC于E、F,已知EF∥BC.
如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB、AC于E、F,已知EF∥BC.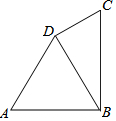 如图,在四边形ABCD中,AB=AD=8cm,∠A=60°,∠BDC=90°,BC=10cm,求△BCD的面积.
如图,在四边形ABCD中,AB=AD=8cm,∠A=60°,∠BDC=90°,BC=10cm,求△BCD的面积.