题目内容
14. 如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB、AC于E、F,已知EF∥BC.
如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB、AC于E、F,已知EF∥BC.(1)求证:BC是⊙O的切线;
(2)若已知AE=9,CF=4,求DE长;
(3)在(2)的条件下,若∠BAC=60°,求tan∠AFE的值及GD长.
分析 (1)连接OD,由角平分线的定义得到∠1=∠2,得到$\widehat{DE}$=$\widehat{DF}$,根据垂径定理得到OD⊥EF,根据平行线的性质得到OD⊥BC,于是得到结论;
(2)连接DE,由$\widehat{DE}$=$\widehat{DF}$,得到DE=DF,根据平行线的性质得到∠3=∠4,等量代换得到∠1=∠4,根据相似三角形的性质即可得到结论;
(3)过F作FH⊥BC于H,由已知条件得到∠1=∠2=∠3=∠4=30°,解直角三角形得到FH=$\frac{1}{2}$DF=$\frac{1}{2}×6$=3,DH=3$\sqrt{3}$,CH=$\sqrt{C{F}^{2}-H{F}^{2}}$=$\sqrt{7}$,根据三角函数的定义得到tan∠AFE=tan∠C=$\frac{HF}{CH}$=$\frac{3\sqrt{7}}{7}$;根据相似三角形到现在即可得到结论.
解答 (1)证明:连接OD,
∵AD是△ABC的角平分线,
∴∠1=∠2,
∴$\widehat{DE}$=$\widehat{DF}$,
∴OD⊥EF,
∵EF∥BC,
∴OD⊥BC,
∴BC是⊙O的切线;
(2)解:连接DE,
∵$\widehat{DE}$=$\widehat{DF}$,
∴DE=DF,
∵EF∥BC,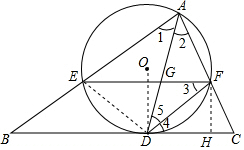
∴∠3=∠4,
∵∠1=∠3,
∴∠1=∠4,
∵∠DFC=∠AED,
∴△AED∽△DFC,
∴$\frac{AE}{DF}=\frac{DE}{CF}$,即$\frac{9}{DE}=\frac{DE}{4}$,
∴DE2=36,
∴DE=6;
(3)解:过F作FH⊥BC于H,
∵∠BAC=60°,
∴∠1=∠2=∠3=∠4=30°,
∴FH=$\frac{1}{2}$DF=$\frac{1}{2}×6$=3,DH=3$\sqrt{3}$,
∴CH=$\sqrt{C{F}^{2}-H{F}^{2}}$=$\sqrt{7}$,
∵EF∥BC,
∴∠C=∠AFE,
∴tan∠AFE=tan∠C=$\frac{HF}{CH}$=$\frac{3\sqrt{7}}{7}$;
∵∠4=∠2.∠C=∠C,
∴△ADC∽△DFC,
∴$\frac{AD}{DF}=\frac{CD}{CF}$,
∵∠5=∠5,∠3=∠2,
∴△ADF∽△FDG,
∴$\frac{AD}{DF}=\frac{DF}{DG}$,
∴$\frac{CD}{CF}$=$\frac{DF}{DG}$,即$\frac{3\sqrt{3}+\sqrt{7}}{4}$=$\frac{6}{DG}$,
∴DG=$\frac{18\sqrt{3}-6\sqrt{7}}{5}$.
点评 本题考查了切线的判定,圆周角定理,相似三角形的判定和性质,解直角三角形,平行线的性质,正确的作出辅助线是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 相等的角是对顶角 | |
| B. | 两条直线被第三条直线所截,内错角相等 | |
| C. | 若两条直线都和第三条直线平行,则这两条直线平行 | |
| D. | 若两个角的和为180°,则这两个角互为邻补角 |
 如图,将连续的奇数1,3,5,7,…按图1中的方式排成一个数表,用一个十字框框住5个数,这样框出的任意5个数(如图2)分别用a,b,c,d,x表示.
如图,将连续的奇数1,3,5,7,…按图1中的方式排成一个数表,用一个十字框框住5个数,这样框出的任意5个数(如图2)分别用a,b,c,d,x表示. 如图,点C把AB分为2:3两段,点D分AB为1:4两段,若DC=5cm,则AD=5cm,AB=25cm.
如图,点C把AB分为2:3两段,点D分AB为1:4两段,若DC=5cm,则AD=5cm,AB=25cm. 如图,正方形ABCD中,P为CD上一动点,过C作CM⊥AP交AP于M并延长AP,使MN=AM,连BD交AN于E,连CN.
如图,正方形ABCD中,P为CD上一动点,过C作CM⊥AP交AP于M并延长AP,使MN=AM,连BD交AN于E,连CN.