Question

1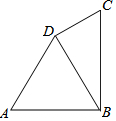．如图，在四边形ABCD中，AB=AD=8cm，∠A=60°，∠BDC=90°，BC=10cm，求△BCD的面积．

Answer 1

分析 证出△ABD为等边三角形．得出BD=8cm．在Rt△BDC中，由勾股定理CD=6cm，即可求出△BCD的面积．

解答 解：∵AB=AD=8cm，∠A=60°，
∴△ABD为等边三角形．
∴BD=AB=8cm．
∵∠BDC=90°，BD=8cm，BC=10cm，
由勾股定理CD=$\sqrt{B{C}^{2}-B{D}^{2}}$=6cm，
∴△BCD的面积=$\frac{1}{2}$ CD×BD=24（cm²）．

点评 本题考查的是勾股定理，等边三角形的判定与性质；熟练掌握勾股定理，证明△ABD是等边三角形是解决问题的关键．