题目内容
20．对于任意整数n，多项式（4n+5）2-9都能（ ）| A． | 被6整除 | B． | 被7整除 | C． | 被8整除 | D． | 被6或8整除 |
分析 根据平方差公式和提公因式法可以解答本题．
解答 解：∵（4n+5）2-9
=[（4n+5）+3][（4n+5）-3]
=（4n+8）（4n+2）
=8（n+2）（2n+1），
∴对于任意整数n，多项式（4n+5）2-9都能倍8整除，
故选C．
点评 本题考查因式分解的应用，解答本题的关键是将题目中的式子进行因式分解，利用整除的性质解答．
练习册系列答案
名校课堂系列答案
相关题目
20．将图1中五边形纸片ABCDE的A点以BE为折线往下折，A点恰好落在CD上，如图2所示，再分别以图2的AB，AE为折线，将C，D两点往上折，使得A、B、C、D、E五点均在同一平面上，如图3所示，若图1中∠A=124°，则图3中∠CAD的度数为何（ ）
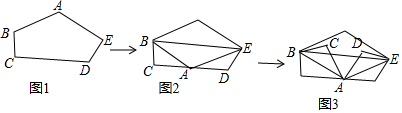
| A． | 56 | B． | 60 | C． | 62 | D． | 68 |
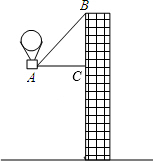如图，有一热气球到达A处时，仪器显示其正前方一高楼顶部B的仰角是43°，与楼的水平距离AC为12米，为了安全飞越高楼，气球应至少再上升多少米？（结果精确到0.1米）
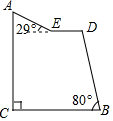“蘑菇石”是我国著名的自然保护区梵净山的标志，小明从山脚B点先乘坐缆车到达观景平台DE观景，然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点，“蘑菇石”A点到水平面BC的垂直距离为1890m．如图，DE∥BC，BD=1800m，∠DBC=80°，求斜坡AE的长度．（结果精确到0.1m，可参考数据sin29°≈0.4848，sin80°≈0.9848，cos29°≈0.8746，cos80°≈0.1736）
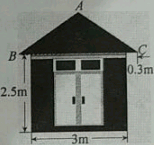一个住宅区的配电房示意图如图所示，它是一个轴对称图形．已知∠ABC=35°，求配电房房顶离地面的高度（精确到0.1m）．（参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70）
将如图所示的正方体的展开图进行折叠后可以围成正方体，则正方体中EF的位置正确的是（ ）
12．关于x的方程（a+3）x2-5x=0的解的情况是（ ）
| A． | 一个解 | B． | 两个解 | C． | 一个或两个解 | D． | 无解 |
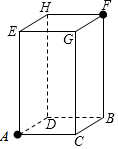一只蚂蚁如果沿长方体的表面从A点爬到F点，那么沿哪条路最近，最短的路程是多少？已知长方体的长2cm、宽为1cm、高为4cm．
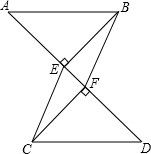如图，已知AB∥CD，BE⊥AD于点E，CF⊥AD于点F，且AF=DE，求证：四边形BECF是平行四边形．