题目内容
10.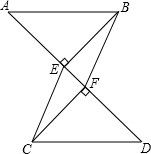 如图,已知AB∥CD,BE⊥AD于点E,CF⊥AD于点F,且AF=DE,求证:四边形BECF是平行四边形.
如图,已知AB∥CD,BE⊥AD于点E,CF⊥AD于点F,且AF=DE,求证:四边形BECF是平行四边形.
分析 通过全等三角形(△AEB≌△DFC)的对应边相等证得BE=CF,由“在同一平面内,同垂直于同一条直线的两条直线相互平行”证得BE∥CF.则四边形BECF是平行四边形.
解答 证明:∵BE⊥AD,CF⊥AD,
∴∠AEB=∠DFC=90°,
∵AB∥CD,
∴∠A=∠D,
∵AF=DE,
∴AE=DF,
在△AEB与△DFC中,
$\left\{\begin{array}{l}{∠AEB=∠DFC}\\{AE=DF}\\{∠A=∠D}\end{array}\right.$,
∴△AEB≌△DFC(ASA),
∴BE=CF.
∵BE⊥AD,CF⊥AD,
∴BE∥CF.
∴四边形BECF是平行四边形.
点评 本题考查了平行四边形的判定、全等三角形的判定与性质.一组对边平行且相等的四边形是平行四边形.

练习册系列答案
相关题目
20.对于任意整数n,多项式(4n+5)2-9都能( )
| A. | 被6整除 | B. | 被7整除 | C. | 被8整除 | D. | 被6或8整除 |
1. 如图,在△ABC中,DE∥BC,若AD=3,BD=4,BC=5,则DE的长为( )
如图,在△ABC中,DE∥BC,若AD=3,BD=4,BC=5,则DE的长为( )
 如图,在△ABC中,DE∥BC,若AD=3,BD=4,BC=5,则DE的长为( )
如图,在△ABC中,DE∥BC,若AD=3,BD=4,BC=5,则DE的长为( )| A. | $\frac{15}{4}$ | B. | $\frac{15}{7}$ | C. | $\frac{12}{5}$ | D. | $\frac{5}{2}$ |
19.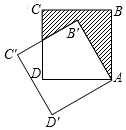 如图,边长为2的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为( )
如图,边长为2的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为( )
 如图,边长为2的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为( )
如图,边长为2的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为( )| A. | 2 | B. | $\frac{3\sqrt{3}}{2}$ | C. | 4-$\frac{4\sqrt{3}}{3}$ | D. | 4-$\frac{3\sqrt{3}}{4}$ |
 如图,PD⊥OA,PE⊥OB,点D,E分别为垂足,且PD=5cm,则当PE=5cm时,点P在∠AOB的平分线上.
如图,PD⊥OA,PE⊥OB,点D,E分别为垂足,且PD=5cm,则当PE=5cm时,点P在∠AOB的平分线上. 在如图所示的正方形网格中,每个小正方形的边长均为1,△ABC的顶点A、C的坐标分别为(-4,5),(-1,3).
在如图所示的正方形网格中,每个小正方形的边长均为1,△ABC的顶点A、C的坐标分别为(-4,5),(-1,3).