题目内容
6.Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2=140°;
(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间有何关系?说明理由.
(3)若点P在Rt△ABC斜边BA的延长线上运动(CE<CD)如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.

分析 (1)连接PC,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠1=∠PCD+∠CPD,∠2=∠PCE+∠CPE,再表示出∠1+∠2即可;
(2)连接PC,方法与(1)相同;
(3)利用三角形的一个外角等于与它不相邻的两个内角的和讨论求解即可.
解答 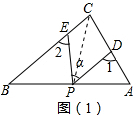 解:(1)如图(1),连接PC,
解:(1)如图(1),连接PC,
由三角形的外角性质,∠1=∠PCD+∠CPD,∠2=∠PCE+∠CPE,
∴∠1+∠2=∠PCD+∠CPD+∠PCE+∠CPE=∠DPE+∠C,
∵∠DPE=∠α=50°,∠C=90°,
∴∠1+∠2=50°+90°=140°,
故答案为:140°;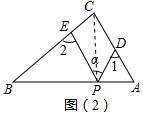
(2)∠1+∠2=90°+∠α;理由如下:
连接PC,如图(2),
由三角形的外角性质,∠1=∠PCD+∠CPD,∠2=∠PCE+∠CPE,
∴∠1+∠2=∠PCD+∠CPD+∠PCE+∠CPE=∠DPE+∠C,
∵∠C=90°,∠DPE=∠α,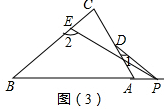
∴∠1+∠2=90°+∠α;
(3)∠2-∠1=90°+∠α或∠2-∠1=90°-α.理由如下:
分情况讨论:
①如图(3),由三角形的外角性质得:∠2=∠C+∠1+∠α,
∴∠2-∠1=90°+∠α;
②当P点运动至ED的延长线时,E,D,P三点共线,
此时∠DPE=0°,
∴∠2-∠1=90°+∠α;
③当P点继续向右运动,此时EP在DP上方,
则∠2-90°=∠1-α,
∴∠2-∠1=90°-α;
综上所述:∠α、∠1、∠2之间的关系为∠2-∠1=90°+∠α或∠2-∠1=90°-α.
点评 此题是三角形综合题,主要考查了四边形的内角和,三角形的内角和,三角形的外角的性质,平角的定义,解本题的关键是将∠1,∠2,α转化到一个三角形或四边形中,是一道比较简单的中考常考题.

练习册系列答案
相关题目
 如图,∠B=62°,∠1=62°,∠D=36°.
如图,∠B=62°,∠1=62°,∠D=36°.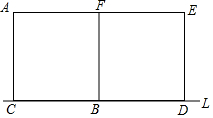 如图,已知边长等于8个单位长度的两个完全相同的正方形ACBF、BDEF有公共边BF,且CB与BD均在直线L上,将正方形ACBF沿直线L以1单位/秒向右平移,设移动时间为t秒,正方形ACBF在移动过程中与正方形BDEF重叠的面积为S,试求:
如图,已知边长等于8个单位长度的两个完全相同的正方形ACBF、BDEF有公共边BF,且CB与BD均在直线L上,将正方形ACBF沿直线L以1单位/秒向右平移,设移动时间为t秒,正方形ACBF在移动过程中与正方形BDEF重叠的面积为S,试求: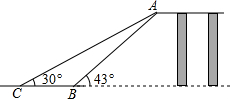 如图是某工厂货物传送带的平面示意图,为提高传送过程的安全性,工厂计划改造传动带与地面的夹角,使其AB的坡角由原来的43°改为30°.已知原传送带AB长为5米.求新旧货物传送带着地点B、C之间相距多远?(结果保留整数,参考数据:sin43°≈0.68,cos43°≈0.73,tan43°≈0.93,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图是某工厂货物传送带的平面示意图,为提高传送过程的安全性,工厂计划改造传动带与地面的夹角,使其AB的坡角由原来的43°改为30°.已知原传送带AB长为5米.求新旧货物传送带着地点B、C之间相距多远?(结果保留整数,参考数据:sin43°≈0.68,cos43°≈0.73,tan43°≈0.93,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)