题目内容
17.在△ABC中,∠C=90°,AB=6,sin∠B=$\frac{1}{3}$,则BC=4$\sqrt{2}$.分析 根据题目中的数据和锐角三角函数可以求得AC的长,然后根据勾股定理即可求得BC的长.
解答 解:∵在△ABC中,∠C=90°,AB=6,sin∠B=$\frac{1}{3}$,
∴sin∠B=$\frac{AC}{AB}$=$\frac{AC}{6}=\frac{1}{3}$,
得AC=2,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}=\sqrt{{6}^{2}-{2}^{2}}$=4$\sqrt{2}$,
故答案为:4$\sqrt{2}$.
点评 本题考查解直角三角形,解答本题的关键是明确题意,利用锐角三角函数和勾股定理解答.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
8.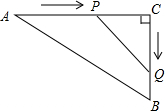 如图,在△ABC中,AC=50m,BC=40m,∠C=90°,点P从点A开始沿AC 边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着射线CB匀速移动,当△PCQ的面积等于300m2运动时间为( )
如图,在△ABC中,AC=50m,BC=40m,∠C=90°,点P从点A开始沿AC 边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着射线CB匀速移动,当△PCQ的面积等于300m2运动时间为( )
 如图,在△ABC中,AC=50m,BC=40m,∠C=90°,点P从点A开始沿AC 边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着射线CB匀速移动,当△PCQ的面积等于300m2运动时间为( )
如图,在△ABC中,AC=50m,BC=40m,∠C=90°,点P从点A开始沿AC 边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着射线CB匀速移动,当△PCQ的面积等于300m2运动时间为( )| A. | 5秒 | B. | 20秒 | C. | 5秒或20秒 | D. | 不确定 |
12.如图所示的立体图形中,含有曲面的是( )


| A. | (1)(2) | B. | (1)(3) | C. | (2)(3) | D. | (2)(4) |
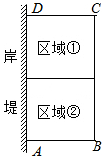 为了节省材料,某水产养殖户利用水库的岸堤为一边,用总长为a米(a为大于21的常数)的围网在水库中围成了如图所示的①②两块矩形区域.已知岸堤的可用长度不超过21米.设AB的长为x米,矩形区域ABCD的面积为y平方米
为了节省材料,某水产养殖户利用水库的岸堤为一边,用总长为a米(a为大于21的常数)的围网在水库中围成了如图所示的①②两块矩形区域.已知岸堤的可用长度不超过21米.设AB的长为x米,矩形区域ABCD的面积为y平方米