题目内容
12.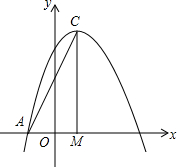 如图,已知抛物线y=-x2+bx+c与x轴的一个交点为A(-1,0),对称轴为直线x=1.
如图,已知抛物线y=-x2+bx+c与x轴的一个交点为A(-1,0),对称轴为直线x=1.(1)求该抛物线的表达式及顶点C的坐标;
(2)设对称轴交x轴于点M,连接AC,CM,请在x轴的正半轴上找一点D,使△ACM与△CMD相似但不全等,求出点D的坐标.
分析 (1)由抛物线的对称轴求出b,代入点A求出c即可;
(2)根据题意分析出点D应在M右侧,且MD和CM是对应边即可求解.
解答 解:(1)抛物线y=-x2+bx+c,对称轴为直线x=1,
可得:$\frac{b}{2}$=1,
解得:b=2,
把A(-1,0)代入:y=-x2+2x+c,
解得:c=3,
∴y=-x2+2x+3,
∵y=-x2+2x+3=-(x-1)2+4,
∴顶点C(1,4);
(2)由x轴的正半轴上一点D,使△ACM与△CMD相似但不全等,
可知点D应在M右侧,且MD和CM是对应边;
如图1,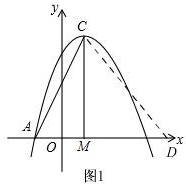
设点D(m,0),
则DM=m-1,CM=4,AM=2,
∵△ACM∽△CDM,
∴$\frac{AM}{CM}=\frac{CM}{DM}$,
∴$\frac{2}{4}=\frac{4}{DM}$,
解得:DM=8,
∴D(9,0).
点评 此题主要考查抛物线与坐标轴的交点问题,会运用对称轴和图象上的点求抛物线解析式,会合理分析相似三角形求出点的坐标是解题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
3.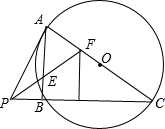 如图,已知:PA切⊙O于A,若AC为⊙O的直径,PBC为⊙O的割线,E为弦AB的中点,PE的延长线交AC于E,且∠FPB=45°,点F到PC的距离为5,则FC的长为( )
如图,已知:PA切⊙O于A,若AC为⊙O的直径,PBC为⊙O的割线,E为弦AB的中点,PE的延长线交AC于E,且∠FPB=45°,点F到PC的距离为5,则FC的长为( )
 如图,已知:PA切⊙O于A,若AC为⊙O的直径,PBC为⊙O的割线,E为弦AB的中点,PE的延长线交AC于E,且∠FPB=45°,点F到PC的距离为5,则FC的长为( )
如图,已知:PA切⊙O于A,若AC为⊙O的直径,PBC为⊙O的割线,E为弦AB的中点,PE的延长线交AC于E,且∠FPB=45°,点F到PC的距离为5,则FC的长为( )| A. | 10 | B. | 12 | C. | $5\sqrt{5}$ | D. | $5\sqrt{6}$ |
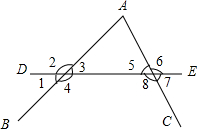 如图,直线DE截AB,AC,构成八个角:
如图,直线DE截AB,AC,构成八个角:
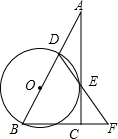 如图,在Rt△ABC中,△ACB=90°,D是AB边上的一点,以BD为直径的⊙O与AC相切于点E,连接DE并延长,与BC的延长线交于点F.
如图,在Rt△ABC中,△ACB=90°,D是AB边上的一点,以BD为直径的⊙O与AC相切于点E,连接DE并延长,与BC的延长线交于点F.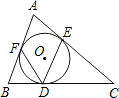 如图,△ABC的内切圆为⊙O,切点分别为D、E、F,若∠A=58°,求∠EDF的度数.
如图,△ABC的内切圆为⊙O,切点分别为D、E、F,若∠A=58°,求∠EDF的度数.