题目内容
7.若单项式-3a4m-nb2与$\frac{1}{3}$a3bm+n是同类项,则这两个单项式的积是( )| A. | -a6b4 | B. | a6b4 | C. | -$\frac{8}{3}$a4b4 | D. | -a3b2 |
分析 根据同类项定义可得$\left\{\begin{array}{l}{4m-n=3}\\{m+n=2}\end{array}\right.$,解出m、n的值,然后可得两个单项式,再求积即可.
解答 解:由题意得:$\left\{\begin{array}{l}{4m-n=3}\\{m+n=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=1}\\{n=1}\end{array}\right.$,
则这两个单项式为-3a3b2与$\frac{1}{3}$a3b2,
-3a3b2•$\frac{1}{3}$a3b2=-a6b4,
故选:A.
点评 此题主要考查了同类项定义和单项式乘法,关键是掌握所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 如图,△ABC中,∠BAC=80°,AB、AC的垂直平分线交于点O,则∠BOC=( )
如图,△ABC中,∠BAC=80°,AB、AC的垂直平分线交于点O,则∠BOC=( )
 如图,△ABC中,∠BAC=80°,AB、AC的垂直平分线交于点O,则∠BOC=( )
如图,△ABC中,∠BAC=80°,AB、AC的垂直平分线交于点O,则∠BOC=( )| A. | 100° | B. | 130° | C. | 160° | D. | 150° |
19. 如图所示,函数y=kx与函数 y=$\frac{12}{x}$交于A、B两点,过点A作AE⊥x轴于点E,AE=4,则B点的坐标为( )
如图所示,函数y=kx与函数 y=$\frac{12}{x}$交于A、B两点,过点A作AE⊥x轴于点E,AE=4,则B点的坐标为( )
 如图所示,函数y=kx与函数 y=$\frac{12}{x}$交于A、B两点,过点A作AE⊥x轴于点E,AE=4,则B点的坐标为( )
如图所示,函数y=kx与函数 y=$\frac{12}{x}$交于A、B两点,过点A作AE⊥x轴于点E,AE=4,则B点的坐标为( )| A. | (4,-3) | B. | (3,4) | C. | (-3,-4) | D. | (4,3) |
17.下列抛物线中,过原点的抛物线是( )
| A. | y=x2-1 | B. | y=(x+1)2 | C. | y=x2+x | D. | y=x2-x-1 |
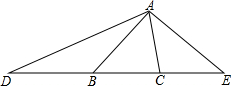 如图,已知:∠ABC=50°,∠ACB=80°,点D、B、C、E四点共线,DB=AB,CE=CA,求∠D、∠E、∠DAE的度数.
如图,已知:∠ABC=50°,∠ACB=80°,点D、B、C、E四点共线,DB=AB,CE=CA,求∠D、∠E、∠DAE的度数.
 如图,电信部门要在公路m,n之间的S区域修建一座电视信号发射塔P.按照设计要求,发射塔P到区域S内的两个城镇A,B的距离必须相等,到两条公路m,n的距离也必须相等.发射塔P应建在什么位置?
如图,电信部门要在公路m,n之间的S区域修建一座电视信号发射塔P.按照设计要求,发射塔P到区域S内的两个城镇A,B的距离必须相等,到两条公路m,n的距离也必须相等.发射塔P应建在什么位置?