题目内容
12.(1)如图(1),在△ABC和△CDE中,已知AC⊥BC,EC⊥DC,且AC=CD,BC=CE,你能判断AB与ED的关系吗?(2)若将△ABC沿CD方向平移得到图(2),请直接判断△ADE的形状,不需要说明理由;若此时EC1=6,AC2=3,你知道线段C1C2的长度吗?说明你的解题思路.
(3)应用上述方法与结论,按照图(3)中的数据,请你直接写出图(3)中实线所围成的图形面积.

分析 (1)由SAS证明△ABC≌△DEC,得出对应边相等即可得出AB=ED;延长BA交ED于M,由直角三角形的性质好对顶角相等证出∠E+∠EAM=90°,得出∠EMA=90°,即可得出AB⊥ED;
(2)同(1)得:△ABC2≌△DEC1,由全等三角形的性质得出C1D=AC2=3,DC2=EC1=6,即可得出C1C2的长;
(3)作AF⊥l于F,DG⊥l于G,BH⊥l于H,由(1)(2)得:△ACF≌△CDG,△DGE≌△EHB,得出CF=DG=3,AF=CG=6,GE=BH=4,EH=DG=3,求出梯形ABHF的面积、△ACF的面积=△CDG的面积、△DEG的面积=△BEH的面积,即可得出实线所围成的图形面积.
解答 解:(1)能判断,AB=ED,AB⊥ED;理由如下: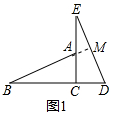
∵AC⊥BC,EC⊥DC,
∴∠ACB=∠DCE=90°,
在△ABC和△DEC中,$\left\{\begin{array}{l}{AC=DC}&{\;}\\{∠ACB=∠DCE}&{\;}\\{BC=EC}&{\;}\end{array}\right.$,
∴△ABC≌△DEC(SAS),
∴AB=ED,∠B=∠E,延长BA交ED于M,如图1所示:
∵∠B+∠BAC=90°,∠EAM=∠BAC,
∴∠E+∠EAM=90°,
∴∠EMA=90°,
∴AB⊥ED;
(2)知道线段C1C2的长度,线段C1C2=6,理由如下:
同(1)得:△ABC2≌△DEC1,
∴C1D=AC2=3,DC2=EC1=6,
∴C1C2=3+6=9;
(3)作AF⊥l于F,DG⊥l于G,BH⊥l于H,如图2所示:
由(1)(2)得:△ACF≌△CDG,△DGE≌△EHB,
∴CF=DG=3,AF=CG=6,GE=BH=4,EH=DG=3,
∴梯形ABHF的面积=$\frac{1}{2}$(6+4)×(3+6+4+3)=80,△ACF的面积=△CDG的面积=$\frac{1}{2}$×6×3=9,△DEG的面积=△BEH的面积=$\frac{1}{2}$×3×4=6,
∴实线所围成的图形面积=80-9-6=65.
点评 本题是三角形综合题目.考查了全等三角形的判定与性质、三角形和梯形面积的计算;本题综合性强,有一定难度,证明三角形全等是解决问题的关键.

| A. | $\sqrt{\frac{2}{3}}$ | B. | $\sqrt{{a}^{2}b}$ | C. | $\sqrt{{a}^{2}{+b}^{2}}$ | D. | $\sqrt{12}$ |
| A. | -a6b4 | B. | a6b4 | C. | -$\frac{8}{3}$a4b4 | D. | -a3b2 |
| A. | 5 | B. | -5 | C. | 5和-5 | D. | 2和3 |
| A. | α=30° | B. | α=45° | C. | 30°<α<45° | D. | 45°<α<60° |
 如图,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,且S△ABC=7,DE=2,AB=4,求AC的长.
如图,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,且S△ABC=7,DE=2,AB=4,求AC的长.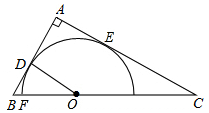 如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=4,AE=6,tan∠BOD=$\frac{2}{3}$.
如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=4,AE=6,tan∠BOD=$\frac{2}{3}$. 如图,将矩形ABCD沿CE向上折叠,使点B落在AD边上的点F处.若AE=3,BE=5,则长AD与宽AB的比值是5:4.
如图,将矩形ABCD沿CE向上折叠,使点B落在AD边上的点F处.若AE=3,BE=5,则长AD与宽AB的比值是5:4.