题目内容
2. 如图,在矩形ABCD中,点E在AD上,且EC平分∠BED,AB=1,∠ABE=45°,则BC的长为( )
如图,在矩形ABCD中,点E在AD上,且EC平分∠BED,AB=1,∠ABE=45°,则BC的长为( )| A. | $\sqrt{2}$ | B. | 1.5 | C. | $\sqrt{3}$ | D. | 2 |
分析 由矩形的性质和角平分线的定义得出∠DEC=∠ECB=∠BEC,推出BE=BC,求得AE=AB=1,然后依据勾股定理可求得BE的长.
解答 解:∵四边形ABCD是矩形,
∴AD∥BC.
∴∠DEC=∠BCE.
∵EC平分∠DEB,
∴∠DEC=∠BEC.
∴∠BEC=∠ECB.
∴BE=BC.
∵四边形ABCD是矩形,
∴∠A=90°.
∵∠ABE=45°,
∴∠ABE=AEB=45°.
∴AB=AE=1.
∵由勾股定理得:BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∴BC=BE=$\sqrt{2}$.
故选:A.
点评 本题考查了矩形的性质,等腰三角形的判定,勾股定理的应用;熟练掌握矩形的性质,证出BE=BC是解题的关键.

练习册系列答案
相关题目
7.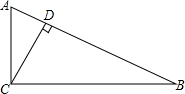 如图,在△ABC中,∠ACB=90°,CD为高,AC=4,则下列计算结果错误的是( )
如图,在△ABC中,∠ACB=90°,CD为高,AC=4,则下列计算结果错误的是( )
 如图,在△ABC中,∠ACB=90°,CD为高,AC=4,则下列计算结果错误的是( )
如图,在△ABC中,∠ACB=90°,CD为高,AC=4,则下列计算结果错误的是( )| A. | 若BC=3,则CD=2.4 | B. | 若∠A=30°,则BD=$\frac{\sqrt{3}}{3}$ | ||
| C. | 若∠A=45°,则AD=2$\sqrt{2}$ | D. | 若BC=2,则S△ADC=$\frac{16}{5}$ |
11.下列运算正确的是( )
| A. | x4+x4=x8 | B. | x2•x=x3 | C. | (x2)3=x5 | D. | x6÷x2=x3 |

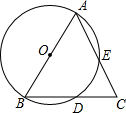 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D、E.
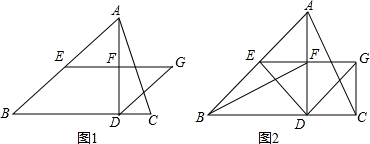
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D、E. 我国古代的数学家很早就发现并应用勾股定理,而且尝试对勾股定理做出证明.最早对勾股定理进行证明的是三国时期吴国的数学家赵爽.如图,就是著名的“赵爽弦图”.△ABE,△BCF,△CDG和△DAH是四个全等的直角三角形,四边形ABCD和EFGH都是正方形.已知AB=5,AH=3,求EF的长.小敏的思路是设EF=x,根据题意,小敏所列的方程是32+(x+3)2=52.
我国古代的数学家很早就发现并应用勾股定理,而且尝试对勾股定理做出证明.最早对勾股定理进行证明的是三国时期吴国的数学家赵爽.如图,就是著名的“赵爽弦图”.△ABE,△BCF,△CDG和△DAH是四个全等的直角三角形,四边形ABCD和EFGH都是正方形.已知AB=5,AH=3,求EF的长.小敏的思路是设EF=x,根据题意,小敏所列的方程是32+(x+3)2=52.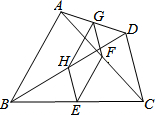 如图,在四边形ABCD中,E,F,G,H分别是BC,AC,AD,BD的中点,要使四边形EFGH是菱形,四边形ABCD的边AB、CD应满足的条件是AB=CD.
如图,在四边形ABCD中,E,F,G,H分别是BC,AC,AD,BD的中点,要使四边形EFGH是菱形,四边形ABCD的边AB、CD应满足的条件是AB=CD.