题目内容
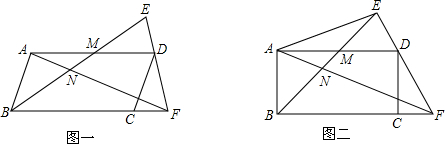
3. 如图,四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处.若AD=5,BC=9,则EF=3$\sqrt{5}$.
如图,四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处.若AD=5,BC=9,则EF=3$\sqrt{5}$.
分析 如图,首先运用翻折变换的性质求出CF、DF的长度,证明∠DEC=90°;运用射影定理求出EF的长度,即可解决问题.
解答  解:如图,由翻折变换的性质得:
解:如图,由翻折变换的性质得:
CF=CB=9,DF=DA=5,∠EFC=∠B=90°;
∠AED=∠FED,∠BEC=∠FEC,
∴∠DEC=$\frac{1}{2}×$180°=90°,即EF⊥CD,
∴由射影定理得:EF2=CF•DF,
∴EF=3$\sqrt{5}$,
故答案为3$\sqrt{5}$.
点评 该题主要考查了翻折变换的性质、射影定理等几何知识点及其应用问题;解题的关键是灵活运用翻折变换的性质、射影定理等几何知识点来分析、判断、推理或解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.如对于任意的实数a、b都有f(a+b)=f(a)+f(b)且f(1)=2,则$\frac{f(2)}{f(1)}$+$\frac{f(4)}{f(2)}$+$\frac{f(6)}{f(3)}$+…+$\frac{f(2012)}{f(1006)}$的值是( )
| A. | 1005 | B. | 1006 | C. | 2012 | D. | 2010 |
18.在数轴上表示不等式x-1<0的解集,正确的是( )
| A. |  | B. |  | C. |  | D. |  |
15.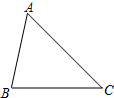 在锐角△ABC中,AB=5,BC=6,∠ACB=45°(如图),将△ABC绕点B按逆时针方向旋转得到△A′BC′(顶点A、C分别与A′、C′对应),当点C′在线段CA的延长线上时,则AC′的长度为( )
在锐角△ABC中,AB=5,BC=6,∠ACB=45°(如图),将△ABC绕点B按逆时针方向旋转得到△A′BC′(顶点A、C分别与A′、C′对应),当点C′在线段CA的延长线上时,则AC′的长度为( )
 在锐角△ABC中,AB=5,BC=6,∠ACB=45°(如图),将△ABC绕点B按逆时针方向旋转得到△A′BC′(顶点A、C分别与A′、C′对应),当点C′在线段CA的延长线上时,则AC′的长度为( )
在锐角△ABC中,AB=5,BC=6,∠ACB=45°(如图),将△ABC绕点B按逆时针方向旋转得到△A′BC′(顶点A、C分别与A′、C′对应),当点C′在线段CA的延长线上时,则AC′的长度为( )| A. | $\sqrt{2}$+$\sqrt{7}$ | B. | 3$\sqrt{2}$-$\sqrt{7}$ | C. | 3$\sqrt{2}$+$\sqrt{7}$ | D. | 3-$\sqrt{7}$ |