题目内容
17.已知抛物线y=2x2-(m+3)x-m+7图象的对称轴为y轴,则m=-3.分析 抛物线的对称轴是y轴,即对称轴是x=0,由对称轴公式列出方程即可求出m.
解答 解:∵抛物线y=2x2-(m+3)x-m+7的对称轴为y轴,
∴-(m+3)=0,
解得:m=-3,
故答案为:-3.
点评 本题主要考查二次函数的性质,掌握抛物线的对称轴公式及及对称轴特点是解题的关键.

练习册系列答案
相关题目
2.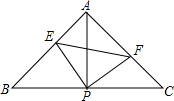 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,PE、PF分别交AB、AC于点E、F.给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF=S△ABC;④EF=AP.上述结论正确的有( )
如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,PE、PF分别交AB、AC于点E、F.给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF=S△ABC;④EF=AP.上述结论正确的有( )
 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,PE、PF分别交AB、AC于点E、F.给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF=S△ABC;④EF=AP.上述结论正确的有( )
如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,PE、PF分别交AB、AC于点E、F.给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF=S△ABC;④EF=AP.上述结论正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.下列方程变形中,正确的是( )
| A. | 方程3x=2,得x=$\frac{3}{2}$ | |
| B. | 方程3-x=2-5(x-1),去括号,得3-x=2-5x-1 | |
| C. | 方程3x-2=2x+1,移项,得3x-2x=-1+2 | |
| D. | 方程$\frac{x-1}{0.2}$-$\frac{x}{0.5}$=1,化成5x-5-2x=1 |
 如图,圆柱形玻璃杯,高为11cm,底面周长为16cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为15cm.(结果保留根号)
如图,圆柱形玻璃杯,高为11cm,底面周长为16cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为15cm.(结果保留根号)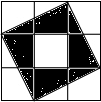 小明把如图所示的3×3的正方形网格纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域(四个全等的直角三角形的每个顶点都在格点上)的概率是$\frac{4}{9}$.
小明把如图所示的3×3的正方形网格纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域(四个全等的直角三角形的每个顶点都在格点上)的概率是$\frac{4}{9}$.