题目内容
6.直径为4的圆内接正三角形的边长为2$\sqrt{3}$.分析 首先根据题意作出图形,然后由垂径定理,可得BD=$\frac{1}{2}$BC,求得∠BOD=$\frac{1}{2}$∠BOC=∠A,再利用三角函数求得BD的长,继而求得答案.
解答  解:如图:△ABC是等边三角形,过点O作OD⊥BC于D,连接OB,OC,
解:如图:△ABC是等边三角形,过点O作OD⊥BC于D,连接OB,OC,
∴BD=CD=$\frac{1}{2}$BC,
∵△ABC是等边三角形,
∴∠A=60°,
∴∠BOC=2∠A=120°,
∴∠BOD=$\frac{1}{2}$∠BOC=60°,
∵直径为4,
∴OB=$\frac{1}{2}$×4=2,
∴BD=OB•sin∠BOD=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴BC=2BD=2$\sqrt{3}$,
即直径为4的圆的内接正三角形的边长为:2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 此题考查了正多边形和圆的性质、垂径定理以及三角函数等知识.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
14.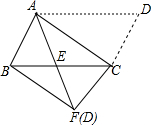 如图,将?ABCD沿对角线AC进行折叠,折叠后点D落在点F处,AF交BC于点E,有下列结论:①△ABF≌△CFB;②AE=CE;③BF∥AC;④BE=CE,其中正确结论的个数是( )
如图,将?ABCD沿对角线AC进行折叠,折叠后点D落在点F处,AF交BC于点E,有下列结论:①△ABF≌△CFB;②AE=CE;③BF∥AC;④BE=CE,其中正确结论的个数是( )
 如图,将?ABCD沿对角线AC进行折叠,折叠后点D落在点F处,AF交BC于点E,有下列结论:①△ABF≌△CFB;②AE=CE;③BF∥AC;④BE=CE,其中正确结论的个数是( )
如图,将?ABCD沿对角线AC进行折叠,折叠后点D落在点F处,AF交BC于点E,有下列结论:①△ABF≌△CFB;②AE=CE;③BF∥AC;④BE=CE,其中正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
16.下列运算正确的是( )
| A. | x3+x2=x5 | B. | x5•x3=x8 | C. | x6÷x2=x3 | D. | (x2)3=x5 |
 如图,在?ABCD中,AC,BD相交于点O,点E是BC边上的中点,且OE=2cm,则边CD的长是4cm.
如图,在?ABCD中,AC,BD相交于点O,点E是BC边上的中点,且OE=2cm,则边CD的长是4cm. 如图所示,已知一次函数y=2x+b的图象与x轴的交点坐标为(-2,0),则不等式2x+b>0的解集为x>-2.
如图所示,已知一次函数y=2x+b的图象与x轴的交点坐标为(-2,0),则不等式2x+b>0的解集为x>-2. 如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB.