题目内容
13. 已知:如图,在平行四边形ABCD 中,E为BC 中点,AE的延长线与DC的延长线相交于点F.求证:DC=CF.
已知:如图,在平行四边形ABCD 中,E为BC 中点,AE的延长线与DC的延长线相交于点F.求证:DC=CF.
分析 利用平行四边形的两组对边分别平行即可得到两角相等,再证明两三角形全等,即可得出结论.
解答 证明:∵四边形ABCD是平行四边形,
∴CD∥AB,AB=CD,
∴∠DFA=∠FAB;
∵E为BC中点,
∴EC=EB,
∴在△ABE与△FCE中,$\left\{\begin{array}{l}{∠DFA=∠FAB}&{\;}\\{∠CEF=∠BEA}&{\;}\\{EB=EC}&{\;}\end{array}\right.$,
∴△ABE≌△FCE(AAS),
∴AB=CF,
∴DC=CF.
点评 此题主要考查平行四边形的性质和判定以及全等三角形的证明,使学生能够灵活运用平行四边形知识解决有关问题.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
5.下列关于$\sqrt{20}$的说法中,错误的是( )
| A. | $\sqrt{20}$是无理数 | B. | 4<$\sqrt{20}$<5 | ||
| C. | $\sqrt{20}$是20的算术平方根 | D. | $\sqrt{20}$不能再化简 |
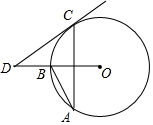 如图,AB、AC是⊙O的两条弦,∠A=30°,过点C的切线与OB的延长线交于点D,则∠D=30°.
如图,AB、AC是⊙O的两条弦,∠A=30°,过点C的切线与OB的延长线交于点D,则∠D=30°.