题目内容
4.问题探究:新定义:
将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“等积线”,其“等积线”被该平面图形截得的线段叫做该平面图形的“等积线段”(例如圆的直径就是圆的“等积线段”).
解决问题:
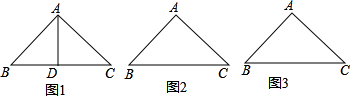
已知在Rt△ABC中,∠BAC=90°,AB=AC=2$\sqrt{2}$.
(1)如图1,若AD⊥BC,垂足为D,则AD是△ABC的一条等积线段,求AD的长;
(2)在图2和图3中,分别画出一条等积线段,并求出它们的长度.(要求:使得图1、图2和图3中的等积线段的长度各不相等)
分析 (1)根据等积线段的定义,可知点D为线段BC的中点,然后根据题目中的条件可以求得AD的长度;
(2)根据题意可以分别画出相应的图形,然后根据相应的图形分别求出相应的等积线段.
解答  解:(1)在Rt△ABC中,
解:(1)在Rt△ABC中,
∵$AC=2\sqrt{2}$,∠C=45°,AD是△ABC的一条等积线段,
∴点D为线段BC的中点,BC=4,
∴AD=2;
(2)符合题意的图形如右上角图2和图3所示:
如图2,当BD是△ABC的一条等积线段时,
∵在Rt△ABC中,∠BAC=90°,AB=AC=2$\sqrt{2}$,BD是△ABC的一条等积线段,
∴点D为AC的中点,
∴AD=$\sqrt{2}$,
∴BD=$\sqrt{(2\sqrt{2})^{2}+(\sqrt{2})^{2}}$=$\sqrt{10}$;
如图3,当DE是△ABC的一条等积线段时,此时DE∥BC,
则△ADE的面积等于△ABC面积的一半,
∵在Rt△ABC中,∠BAC=90°,AB=AC=2$\sqrt{2}$,
∴△ABC的面积为:$\frac{2\sqrt{2}×2\sqrt{2}}{2}=4$,
∴△ADE的面积是2,
设AD=a,
则 $\frac{{a}^{2}}{2}=2$,得a2=4,
∴DE=$\sqrt{{a}^{2}+{a}^{2}}=\sqrt{2{a}^{2}}=\sqrt{2×4}=2\sqrt{2}$.
点评 本题考查相似三角形的判定与性质、等腰三角形、新定义、勾股定理,解题的关键是明确题目中等积线段的定义,利用数形结合的思想解答问题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
15. 如图,∠O=∠1,∠2=∠3,∠4=∠5,∠6=∠7,∠8=90°.则∠O的度数为( )
如图,∠O=∠1,∠2=∠3,∠4=∠5,∠6=∠7,∠8=90°.则∠O的度数为( )
 如图,∠O=∠1,∠2=∠3,∠4=∠5,∠6=∠7,∠8=90°.则∠O的度数为( )
如图,∠O=∠1,∠2=∠3,∠4=∠5,∠6=∠7,∠8=90°.则∠O的度数为( )| A. | 10° | B. | 15° | C. | 18° | D. | 20° |
16. 如图,点A(1.5,3)在第一象限,OA与x轴所夹的锐角为α,tanα=( )
如图,点A(1.5,3)在第一象限,OA与x轴所夹的锐角为α,tanα=( )
 如图,点A(1.5,3)在第一象限,OA与x轴所夹的锐角为α,tanα=( )
如图,点A(1.5,3)在第一象限,OA与x轴所夹的锐角为α,tanα=( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 3 |
 如图,直三棱柱ABC-A1B1C1的侧棱长和底面各边长均为2,其主视图是边长为2的正方形,则此直三棱柱左视图的面积为多少?
如图,直三棱柱ABC-A1B1C1的侧棱长和底面各边长均为2,其主视图是边长为2的正方形,则此直三棱柱左视图的面积为多少?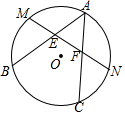 如图所示,AB、AC是⊙O的两条弦.M、N分别是$\widehat{AB}$、$\widehat{AC}$的中点,MN交AB、AC于点E、F.求证:△AEF是等腰三角形.
如图所示,AB、AC是⊙O的两条弦.M、N分别是$\widehat{AB}$、$\widehat{AC}$的中点,MN交AB、AC于点E、F.求证:△AEF是等腰三角形.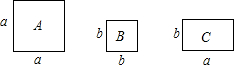 如图,有正方形卡片A类、B类和长方形卡片C类各若干张,如果用这三类卡片拼一个长为2a+b、宽为a+2b的大长方形,通过计算说明三类卡片各需多少张?
如图,有正方形卡片A类、B类和长方形卡片C类各若干张,如果用这三类卡片拼一个长为2a+b、宽为a+2b的大长方形,通过计算说明三类卡片各需多少张? 已知:如图,在平行四边形ABCD 中,E为BC 中点,AE的延长线与DC的延长线相交于点F.求证:DC=CF.
已知:如图,在平行四边形ABCD 中,E为BC 中点,AE的延长线与DC的延长线相交于点F.求证:DC=CF.