题目内容
若一个二次函数y=ax2-4ax+3（a≠0）的图象经过两点A（m+2，y1）、B（2-m，y2），则下列关系正确的是（ ）
| A、y1＞y2 |
| B、y1＜y2 |
| C、y1=y2 |
| D、y1≥y2 |
考点：二次函数图象上点的坐标特征
专题：计算题
分析：根据二次函数的性质先确定抛物线的对称轴为直线x=2，然后根据点A和点B到直线x=2的距离的远近进行判断．
解答：解：抛物线的对称轴为直线x=-
=2，
∵点A（m+2，y1）、B（2-m，y2）到直线x=2的距离相等，
∴y1=y2．
故选C．
| -4a |
| 2a |
∵点A（m+2，y1）、B（2-m，y2）到直线x=2的距离相等，
∴y1=y2．
故选C．
点评：本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．也考查了二次函数的性质．
练习册系列答案
相关题目
下列计算正确的是（ ）
| A、（x+y）2=x2+y2 |
| B、（x-y）2=x2-2xy-y2 |
| C、（-x+y）2=x2-2xy+y2 |
| D、（x+2y）（x-2y）=x2-2y2 |
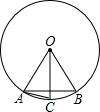如图，在⊙O中，OA=AB，OC⊥AB，则下列结论错误的是（ ）| A、弧AC=弧BC |
| B、△OAB是等边三角形 |
| C、AC=BC |
| D、∠BAC=30° |
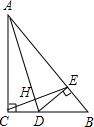已知：如图，在△ABC中，∠ACB=90°，∠CAB的平分线交BC于D，DE⊥AB，垂足为E，连结CE，交AD于点H．
周末，甲、乙两组同学从校出发，前往同一景点郊游，甲组同学骑电动车先行，1h后乙组同学乘车前往，图中表示的是甲、乙两组同学各自到达景点的距离s（km）与所用时间t（h）的函数图象，根据已给信息，解答以下问题：