题目内容
6.如图1,AB为⊙O的直径,直线CD切⊙O于点C,AD⊥CD于点D,交⊙O于点E.(1)求证:AC平分∠DAB;
(2)若4AB=5AD,求证:AE=3DE;
(3)如图2,在(2)的条件下,CF交⊙O于点F,若AB=10,∠ACF=45°,求CF的长.
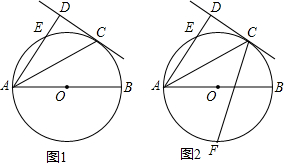
分析 (1)连接OC,如图1①,易证OC∥AD,只需结合OA=OC就可解决问题;
(2)连接BC、EC、OC,如图1②,设AB=5x,由4AB=5AD可得AD=4x,易证△ADC∽△ACB,根据相似三角形的性质可求出DC2(用x表示),然后运用切割线定理求出DE,即可得到AE,问题得以解决;
(3)过点A作AH⊥FC,连接AF,如图2,由条件AB=10可求出x,从而可求出AC、AF,然后只需解△ACF就可解决问题.
解答 解:(1)连接OC,如图1①,
∵CD为⊙O的切线,
∴OC⊥CD.
∵AD⊥CD,
∴OC∥AD,
∴∠CAD=∠ACO.
又∵OC=OA,
∴∠ACO=∠OAC,
∴∠CAD=∠OAC,
∴AC平分∠DAB;
(2)连接BC、EC、OC,如图1②,
设AB=5x,则由4AB=5AD可得AD=4x.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ADC=∠ACB=90°.
∵∠DAC=∠CAB,
∴△ADC∽△ACB,
∴$\frac{AD}{AC}$=$\frac{AC}{AB}$,
∴AC2=AD•AB=20x2,
∴DC2=AC2-AD2=20x2-16x2=4x2.
∵直线CD与⊙O相切,
∴根据切割线定理可得CD2=DE•DA,
∴4x2=DE•4x,
∴DE=x,
∴AE=3x=3DE;
(3)过点A作AH⊥FC,连接AF,如图2,
∵AB=5x=10,
∴OA=OF=5,x=2,
∴AC2=20x2=80,
∴AC=4$\sqrt{5}$.
∵∠ACF=45°,
∴AH=AC•sin∠ACH=4$\sqrt{5}$×$\frac{\sqrt{2}}{2}$=2$\sqrt{10}$,
CH=AC•cos∠ACH=4$\sqrt{5}$×$\frac{\sqrt{2}}{2}$=2$\sqrt{10}$.
∵∠AOF=2∠ACF=90°,
∴AF=$\sqrt{{5}^{2}+{5}^{2}}$=5$\sqrt{2}$,
∴FH=$\sqrt{A{F}^{2}-A{H}^{2}}$=$\sqrt{10}$,
∴FC=CH+FH=3$\sqrt{10}$,
即CF的长为3$\sqrt{10}$.
点评 本题主要考查了切线的性质、圆周角定理、切割线定理、三角函数、相似三角形的判定与性质、勾股定理、解三角形、平行线的判定与性质等知识,把求CF转化为解△ACF是解决第(3)小题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | 直角 | B. | 钝角 | ||
| C. | 锐角 | D. | 以上三种情况都有可能 |
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | $-\frac{1}{2}$ |
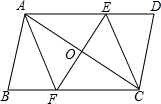 已知:如图,在?ABCD中,线段EF分别交AD、AC、BC于点E、O、F,EF⊥AC,AO=CO.
已知:如图,在?ABCD中,线段EF分别交AD、AC、BC于点E、O、F,EF⊥AC,AO=CO. 已知:如图,直线a、b、c两两相交,∠1=2∠3,∠2=86°.求∠4的度数.
已知:如图,直线a、b、c两两相交,∠1=2∠3,∠2=86°.求∠4的度数. 如图,在△ABC中,BO平分∠ABC,CQ平分∠ACB,DE过O且平行于BC,已知△ADE的周长为10cm,BC的长为5cm,则△ABC的周长是15cm.
如图,在△ABC中,BO平分∠ABC,CQ平分∠ACB,DE过O且平行于BC,已知△ADE的周长为10cm,BC的长为5cm,则△ABC的周长是15cm.