题目内容
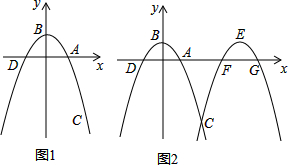
14. 如图1,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3;如图2,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为S4、S5、S6.其中S1=16,S2=45,S5=11,S6=14,则S3+S4=( )
如图1,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3;如图2,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为S4、S5、S6.其中S1=16,S2=45,S5=11,S6=14,则S3+S4=( )| A. | 86 | B. | 64 | C. | 54 | D. | 48 |
分析 分别用AB、BC和AC表示出 S1、S2、S3,然后根据AB2=AC2+BC2即可得出S1、S2、S3的关系.同理,得出S4、S5、S6的关系.
解答  解:如图1,S1=$\frac{\sqrt{3}}{4}$AC2,S2=$\frac{\sqrt{3}}{4}$AB2,S3=$\frac{\sqrt{3}}{4}$BC2,
解:如图1,S1=$\frac{\sqrt{3}}{4}$AC2,S2=$\frac{\sqrt{3}}{4}$AB2,S3=$\frac{\sqrt{3}}{4}$BC2,
∵BC2=AB2-AC2,
∴S2-S1=S3,
如图2,S4=S5+S6,
∴S3+S4=45-16+11+14=54.
故选C.
点评 本题考查了勾股定理、等边三角形的性质.勾股定理:如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.

练习册系列答案
相关题目
4.下列说法正确的是( )
| A. | 要了解人们对“低碳生活”的了解程度,宜采用普查方式 | |
| B. | 一组数据5,5,6,7的众数和中位数都是5 | |
| C. | 必然事件发生的概率为100% | |
| D. | 若甲组数据的方差是3.4,乙组数据的方差是1.68,则甲组数据比乙组数据稳定 |
5.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
9.若正比例函数y=kx的图象经过点(2,-6),则k的值为( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | 3 | D. | $\frac{1}{3}$ |
19.若$\sqrt{m-8}$+|n-2|=0,且二次函数y=ax2+mx+n与x轴有交点,则a的取值范围是( )
| A. | a<8且a≠0 | B. | a≥8 | C. | a≤8且a≠0 | D. | a≤8 |
4.不等式组$\left\{\begin{array}{l}{2x-1≤3}\\{x+3>4}\end{array}\right.$的解集是( )
| A. | x>1 | B. | 1<x≤2 | C. | x≤2 | D. | 无解 |
 如图,某数学兴趣小组将边长为5的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ABD的面积为25.
如图,某数学兴趣小组将边长为5的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ABD的面积为25.