题目内容
3. 如图,某数学兴趣小组将边长为5的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ABD的面积为25.
如图,某数学兴趣小组将边长为5的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ABD的面积为25.
分析 根据扇形面积公式:S=$\frac{1}{2}$•L•R(L是弧长,R是半径),求出弧长BD,根据题意$\widehat{BD}$=CD+BC,由此即可解决问题.
解答 解:由题意$\widehat{DB}$=CD+BC=10,
S扇形ADB=$\frac{1}{2}$•$\widehat{BD}$•AB=$\frac{1}{2}$×10×5=25,
故答案为25.
点评 本题考查扇形面积公式,解题的关键是记住扇形面积公式S=$\frac{nπ{R}^{2}}{360}$=$\frac{1}{2}$LR,属于中考常考题型.

练习册系列答案
相关题目
14. 如图1,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3;如图2,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为S4、S5、S6.其中S1=16,S2=45,S5=11,S6=14,则S3+S4=( )
如图1,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3;如图2,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为S4、S5、S6.其中S1=16,S2=45,S5=11,S6=14,则S3+S4=( )
 如图1,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3;如图2,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为S4、S5、S6.其中S1=16,S2=45,S5=11,S6=14,则S3+S4=( )
如图1,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3;如图2,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为S4、S5、S6.其中S1=16,S2=45,S5=11,S6=14,则S3+S4=( )| A. | 86 | B. | 64 | C. | 54 | D. | 48 |
11.不等式2x>-3的解是( )
| A. | x<$-\frac{3}{2}$ | B. | x>-$\frac{3}{2}$ | C. | x<-$\frac{2}{3}$ | D. | x>-$\frac{2}{3}$ |
15. 如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M到坐标原点O的距离是( )
如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M到坐标原点O的距离是( )
 如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M到坐标原点O的距离是( )
如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M到坐标原点O的距离是( )| A. | 10 | B. | 8$\sqrt{2}$ | C. | 4$\sqrt{13}$ | D. | 2$\sqrt{41}$ |
12.下列运算结果为x-1的是( )
| A. | 1-$\frac{1}{x}$ | B. | $\frac{{x}^{2}-1}{x}$•$\frac{x}{x+1}$ | C. | $\frac{x+1}{x}$÷$\frac{1}{x-1}$ | D. | $\frac{{x}^{2}+2x+1}{x+1}$ |

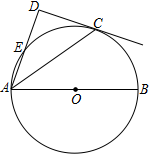 如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.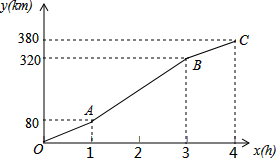 暑假期间,小刚一家乘车去离家380公里的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.
暑假期间,小刚一家乘车去离家380公里的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.