题目内容
4．不等式组$\left\{\begin{array}{l}{2x-1≤3}\\{x+3＞4}\end{array}\right.$的解集是（ ）| A． | x＞1 | B． | 1＜x≤2 | C． | x≤2 | D． | 无解 |
分析 分别求出不等式组中两不等式的解集，找出解集的公共部分即可．
解答 解：$\left\{\begin{array}{l}{2x-1≤3①}\\{x+3＞4②}\end{array}\right.$，
由①得：x≤2，
由②得：x＞1，
则不等式组的解集为1＜x≤2，
故选B
点评 此题考查了解一元一次不等式组，熟练掌握运算法则是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
14．
如图1，分别以直角三角形三边为边向外作等边三角形，面积分别为S1、S2、S3；如图2，分别以直角三角形三个顶点为圆心，三边长为半径向外作圆心角相等的扇形，面积分别为S4、S5、S6．其中S1=16，S2=45，S5=11，S6=14，则S3+S4=（ ）
如图1，分别以直角三角形三边为边向外作等边三角形，面积分别为S1、S2、S3；如图2，分别以直角三角形三个顶点为圆心，三边长为半径向外作圆心角相等的扇形，面积分别为S4、S5、S6．其中S1=16，S2=45，S5=11，S6=14，则S3+S4=（ ）| A． | 86 | B． | 64 | C． | 54 | D． | 48 |
15．
如图，在平面直角坐标系中，⊙M与x轴相切于点A（8，0），与y轴分别交于点B（0，4）和点C（0，16），则圆心M到坐标原点O的距离是（ ）
如图，在平面直角坐标系中，⊙M与x轴相切于点A（8，0），与y轴分别交于点B（0，4）和点C（0，16），则圆心M到坐标原点O的距离是（ ）| A． | 10 | B． | 8$\sqrt{2}$ | C． | 4$\sqrt{13}$ | D． | 2$\sqrt{41}$ |
12．下列运算结果为x-1的是（ ）
| A． | 1-$\frac{1}{x}$ | B． | $\frac{{x}^{2}-1}{x}$•$\frac{x}{x+1}$ | C． | $\frac{x+1}{x}$÷$\frac{1}{x-1}$ | D． | $\frac{{x}^{2}+2x+1}{x+1}$ |
如图，已知菱形ABCD的两条对角线长分别为AC=8和BD=6，那么，菱形ABCD的面积为24．
16．若-x3ya与xby是同类项，则a+b的值为（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
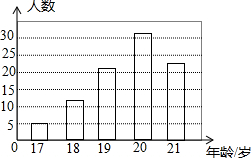在6月26日“国际禁毒日”来临之际，华明中学围绕“珍爱生命，远离毒品”主题，组织师生到当地戒毒所开展相关问题的问卷调查活动，其中“初次吸毒时的年龄”在17至21岁的统计结果如图所示，则这些年龄的众数是（ ）