题目内容
19．若$\sqrt{m-8}$+|n-2|=0，且二次函数y=ax2+mx+n与x轴有交点，则a的取值范围是（ ）| A． | a＜8且a≠0 | B． | a≥8 | C． | a≤8且a≠0 | D． | a≤8 |
分析 利用非负数的性质求得m、n的值；然后将其代入二次函数解析式，利用抛物线与x轴交点的条件来求a的取值范围．
解答 解：∵$\sqrt{m-8}$+|n-2|=0，
∴m-8=0，n-2=0，
解得m=8，n=2，
则该二次函数是y=ax2+8x+2，
∵该二次函数图象与x轴有交点，
∴△=82-4a×2≥0且a≠0，
解得a≤8且a≠0．
故选：C．
点评 本题考查了抛物线与x轴的交点，非负数的性质．该题属于易错题，同学们解题时，往往忽略了二次函数的定义，导致a的取值范围解答错误，误选D选项．
练习册系列答案
相关题目
10．要使式子$\frac{{\sqrt{x-1}}}{x-3}$-x+2有意义，则x的取值范围是（ ）
| A． | x＞1 | B． | x≥1 | C． | x≥1且x≠3 | D． | x≥3 |
如图是由几个相同的小正方体搭成的一个几何体，它的俯视图是（ ）
14．
如图1，分别以直角三角形三边为边向外作等边三角形，面积分别为S1、S2、S3；如图2，分别以直角三角形三个顶点为圆心，三边长为半径向外作圆心角相等的扇形，面积分别为S4、S5、S6．其中S1=16，S2=45，S5=11，S6=14，则S3+S4=（ ）
如图1，分别以直角三角形三边为边向外作等边三角形，面积分别为S1、S2、S3；如图2，分别以直角三角形三个顶点为圆心，三边长为半径向外作圆心角相等的扇形，面积分别为S4、S5、S6．其中S1=16，S2=45，S5=11，S6=14，则S3+S4=（ ）| A． | 86 | B． | 64 | C． | 54 | D． | 48 |
4．我市飞鹤中学初三（一）班某小组7位学生的中考体育测试成绩（满分30分）依次为27，30，29，27，30，28，30．则这组数据的众数与中位数分别是（ ）
| A． | 30，27 | B． | 30，29 | C． | 29，30 | D． | 30，28 |
11．不等式2x＞-3的解是（ ）
| A． | x＜$-\frac{3}{2}$ | B． | x＞-$\frac{3}{2}$ | C． | x＜-$\frac{2}{3}$ | D． | x＞-$\frac{2}{3}$ |
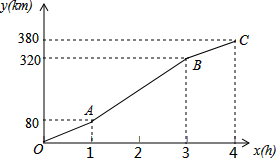暑假期间，小刚一家乘车去离家380公里的某景区旅游，他们离家的距离y（km）与汽车行驶时间x（h）之间的函数图象如图所示．