题目内容
2.在一个不透明的袋子中装有四个小球,它们除分别标有的号码1,2,3,4不同外,其他完全相同.任意从袋子中摸出一球后不放回,再任意摸出一球,则第二次摸出球的号码比第一次摸出球的号码大的概率是$\frac{1}{2}$.分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与第二次摸出球的号码比第一次摸出球的号码大的情况,再利用概率公式求解即可求得答案.
解答 解:画树状图得:
∵共有12种等可能的结果,第二次摸出球的号码比第一次摸出球的号码大的有6种情况,
∴第二次摸出球的号码比第一次摸出球的号码大的概率是:$\frac{6}{12}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
10.要使式子$\frac{{\sqrt{x-1}}}{x-3}$-x+2有意义,则x的取值范围是( )
| A. | x>1 | B. | x≥1 | C. | x≥1且x≠3 | D. | x≥3 |
17.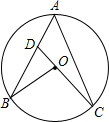 如图,点A、B、C在⊙O上,CO的延长线交AB于点D,BD=BO,∠A=50°,则∠B的度数为( )
如图,点A、B、C在⊙O上,CO的延长线交AB于点D,BD=BO,∠A=50°,则∠B的度数为( )
 如图,点A、B、C在⊙O上,CO的延长线交AB于点D,BD=BO,∠A=50°,则∠B的度数为( )
如图,点A、B、C在⊙O上,CO的延长线交AB于点D,BD=BO,∠A=50°,则∠B的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
14. 如图1,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3;如图2,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为S4、S5、S6.其中S1=16,S2=45,S5=11,S6=14,则S3+S4=( )
如图1,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3;如图2,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为S4、S5、S6.其中S1=16,S2=45,S5=11,S6=14,则S3+S4=( )
 如图1,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3;如图2,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为S4、S5、S6.其中S1=16,S2=45,S5=11,S6=14,则S3+S4=( )
如图1,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3;如图2,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为S4、S5、S6.其中S1=16,S2=45,S5=11,S6=14,则S3+S4=( )| A. | 86 | B. | 64 | C. | 54 | D. | 48 |
11.不等式2x>-3的解是( )
| A. | x<$-\frac{3}{2}$ | B. | x>-$\frac{3}{2}$ | C. | x<-$\frac{2}{3}$ | D. | x>-$\frac{2}{3}$ |
12.下列运算结果为x-1的是( )
| A. | 1-$\frac{1}{x}$ | B. | $\frac{{x}^{2}-1}{x}$•$\frac{x}{x+1}$ | C. | $\frac{x+1}{x}$÷$\frac{1}{x-1}$ | D. | $\frac{{x}^{2}+2x+1}{x+1}$ |

 如图是由几个相同的小正方体搭成的一个几何体,它的俯视图是( )
如图是由几个相同的小正方体搭成的一个几何体,它的俯视图是( )


