题目内容
 如图,在Rt△ABC中,∠C=90°,AB=15,sin∠BAC=
如图,在Rt△ABC中,∠C=90°,AB=15,sin∠BAC=| 3 |
| 5 |
考点:解直角三角形
专题:
分析:先解Rt△ABC,得出BC、AC的长度,再由BD=4,求出CD,然后根据正切函数的定义即可求出tan∠ADC的值.
解答:解:在Rt△ABC中,∵∠C=90°,AB=15,sin∠BAC=
,
∴BC=AB•sin∠BAC=15×
=9,
∴AC=
=
=12,
∵BD=4,
∴CD=BC-BD=9-4=5,
∴tan∠ADC=
=
.
| 3 |
| 5 |
∴BC=AB•sin∠BAC=15×
| 3 |
| 5 |
∴AC=
| AB2-BC2 |
| 152-92 |
∵BD=4,
∴CD=BC-BD=9-4=5,
∴tan∠ADC=
| AC |
| CD |
| 12 |
| 5 |
点评:本题考查了解直角三角形以及三角函数的定义,在直角三角形中,正弦值等于对边比斜边,正切值等于对边比邻边.

练习册系列答案
相关题目
 某中学部分同学参加全国初中数学竞赛,取得了优异的成绩,指导教师统计了所有参赛同学的成绩(成绩都是整数,试题满分120分),并且绘制了频率分布直方图,根据图中提供的信息回答下列问题:
某中学部分同学参加全国初中数学竞赛,取得了优异的成绩,指导教师统计了所有参赛同学的成绩(成绩都是整数,试题满分120分),并且绘制了频率分布直方图,根据图中提供的信息回答下列问题: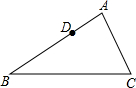 如图,在△ABC中,AB=4,AC=3,D、E分别是AB、AC上的动点,在边AC上取一点E,使A、D、E三点组成的三角形与△ABC相似.
如图,在△ABC中,AB=4,AC=3,D、E分别是AB、AC上的动点,在边AC上取一点E,使A、D、E三点组成的三角形与△ABC相似. 如图,A是正方体小木块(质地均匀)的一顶点,将其随机投掷在水平桌面上,则A点的棱长与桌面接触的概率
如图,A是正方体小木块(质地均匀)的一顶点,将其随机投掷在水平桌面上,则A点的棱长与桌面接触的概率