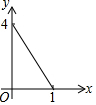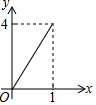题目内容
8.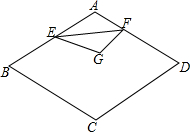 如图,已知菱形ABCD中,∠BAD=120°,AB=2,E、F分别是线段AB、AD上的动点,若以EF为折线翻折,点A落在菱形ABCD所在平面的G点位置,则点G所有可能出现的区域的面积是$\frac{4}{3}$π-2$\sqrt{3}$.
如图,已知菱形ABCD中,∠BAD=120°,AB=2,E、F分别是线段AB、AD上的动点,若以EF为折线翻折,点A落在菱形ABCD所在平面的G点位置,则点G所有可能出现的区域的面积是$\frac{4}{3}$π-2$\sqrt{3}$.
分析 以EF为折线翻折,A点落在菱形ABCD所在的G点的位置,那么G所有可能位置形成的图形是图中阴影部分.根据S阴=2•S扇形BAC-S菱形ABCD计算即可.
解答 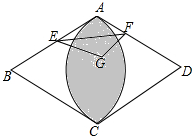 解:如图,以EF为折线翻折,点A落在菱形ABCD所在平面的G点位置,
解:如图,以EF为折线翻折,点A落在菱形ABCD所在平面的G点位置,
则点G所有可能出现的区域是图中阴影.
∵四边形ABCD是菱形,∠BAD=120°,
∴∠B=60°,
∴S阴=2•S扇形BAC-S菱形ABCD=2×$\frac{60π×{2}^{2}}{360}$-2×$\sqrt{3}$=$\frac{4}{3}$π-2$\sqrt{3}$,
故答案为:$\frac{4}{3}$π-2$\sqrt{3}$.
点评 本题考查翻折变换、扇形的面积公式、菱形的性质等知识,解题的关键是正确判断G所有可能位置形成的图形,属于中考填空题中的压轴题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
13.安徽省作为首批国家电子商务进农村示范省之一,先后携手阿里巴巴、苏宁云商等电商巨头,推动线上线下融合发展,激发农村消费潜力,实现“安徽特产卖全国”.根据某淘宝农村超市统计一月份的营业额为36万元,三月份的营业额为49万元.设每月的平均增长率为x,则可列方程为( )
| A. | 49(1+x)2=36 | B. | 36(1-x)2=49 | C. | 36(1+x)2=49 | D. | 49(1-x)2=36 |
20.揭西县是全国著名的侨乡,拥有海外华侨、华人及港、澳、台同胞共608000人,这一数据用科学记数法表示为( )
| A. | 0.608×106 | B. | 6.08×105 | C. | 6.08×106 | D. | 60.8×104 |
18. 如图,AB∥CD,∠CDE=130°,则∠A的度数是( )
如图,AB∥CD,∠CDE=130°,则∠A的度数是( )
 如图,AB∥CD,∠CDE=130°,则∠A的度数是( )
如图,AB∥CD,∠CDE=130°,则∠A的度数是( )| A. | 130° | B. | 50° | C. | 70° | D. | 30° |
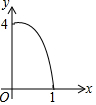
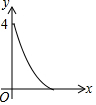
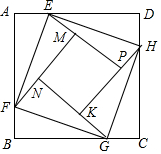 如图正方形ABCD的边长为2,点E,F,G,H分别在AD,AB,BC,CD上,且EA=FB=GC=HD,分别将△AEF,△BFG,△CGH,△DHE沿EF,FG,GH,HE翻折,得四边形MNKP,设AE=x(0<x<1),S四边形MNKP=y,则y关于x的函数图象大致为( )
如图正方形ABCD的边长为2,点E,F,G,H分别在AD,AB,BC,CD上,且EA=FB=GC=HD,分别将△AEF,△BFG,△CGH,△DHE沿EF,FG,GH,HE翻折,得四边形MNKP,设AE=x(0<x<1),S四边形MNKP=y,则y关于x的函数图象大致为( )