题目内容
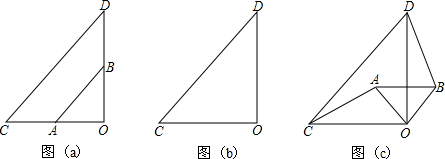
9. 如图,△ABC和△ADE都是等边三角形,且点B,A,E在同一直线上,连接BD交AC于M,连接CE交AD于N,连接MN.
如图,△ABC和△ADE都是等边三角形,且点B,A,E在同一直线上,连接BD交AC于M,连接CE交AD于N,连接MN.(1)求证:BD=CE;
(2)求证:BM=CN;
(3)求证:MN∥BE.
(4)若点P,Q分别是BD,CE的中点,试判断△PAQ的形状,并证明你的结论.
分析 (1)由已知条件利用SAS证明△ABD≌△ACE即可.
(2)由已知条件利用ASA证明△ABM≌△ACN.
(3)在(2)的基础上可利用内错角证明MN∥BE.
(4)由(1)得出的结论得出∠ADB=∠AEC,BD=CE,进而判断出△PDA≌△QEA即可得出AP=AQ,∠DPA=∠QEA,最后判断出∠PAQ=60°即可.
解答 证明:(1)∵△ABC和△ADE都是等边三角形,
则在△ABD和△ACE中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$
∴△ABD≌△ACE,
∴BD=CE.
(2)由(1)可知,∠DBA=∠ACE,
又∵AB=AC,∠BAC=∠CAD=60°,
则在△ABM和△ACN中,$\left\{\begin{array}{l}{∠DBA=∠ACE}\\{AB=AC}\\{∠BAC=∠CAD}\end{array}\right.$
∴△ABM≌△ACN,
∴BM=CN.
(3)由(2)得,AM=AN,
∴∠AMN=∠ANM=60°=∠DAE,
∴MN∥BE.
(4)由(1)知,△ABD≌△ACE(SAS),
∴∠ADB=∠AEC,BD=CE,
∵P,Q分别为DD,CE的中点,
∴DP=EQ,
在△PDA和△QEA中 $\left\{\begin{array}{l}{DP=EQ}\\{∠BDA=∠CEA}\\{DA=EA}\end{array}\right.$
∴△PDA≌△QEA,
∴AP=AQ,∠DPA=∠QEA,
∵∠QAE+∠DAQ=60°,
∴∠PAD+∠DAQ=60°,
即∠PAQ=60°,
在△PAQ中,AP=AQ,∠PAQ=60°,
∴△PAQ为正三角形
点评 本题是三角形综合题,主要考查看了全等三角形的判定和性质,等边三角形的性质,线段中点的定义,三角形的内角和定理,准确的找出全等三角形是解题的关键.

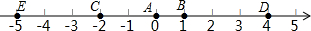 如图,A点的初始位置位于数轴上的原点.现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样.
如图,A点的初始位置位于数轴上的原点.现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样.

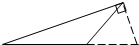
 如图所示,?ABCD中,G是BC延长线上的一点,AG与BD交于点E,与DC交于点F,此图中的相似三角形共有6对.
如图所示,?ABCD中,G是BC延长线上的一点,AG与BD交于点E,与DC交于点F,此图中的相似三角形共有6对.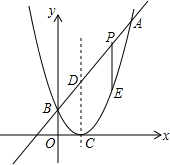 如图,己知二次函数图象的顶点坐标为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,与对称轴交于D(m,2),其中B点在y轴上
如图,己知二次函数图象的顶点坐标为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,与对称轴交于D(m,2),其中B点在y轴上