题目内容
20.已知a+b=3,ab=-12,求下列各式的值(1)a2+b2
(2)a2-ab+b2.
分析 (1)先根据完全平方公式进行变形,再代入求出即可;
(2)先根据完全平方公式进行变形,再代入求出即可.
解答 解:(1)∵a+b=3,ab=-12,
∴a2+b2=(a+b)2-2ab=32-2×(-12)=33;
(2)∵a+b=3,ab=-12,
∴a2-ab+b2=(a+b)2-3ab=32-3×(-12)=45.
点评 本题考查了完全平方公式的应用,能灵活运用公式进行变形是解此题的关键,注意:(a+b)2=a2+2ab+b2.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
10.将自然数按如图所示的方式排列.
第1列 第2列 第3列 第4列
第一行 0
第二行 1 2
第三行 2 3 4
第四行 3 4 5 6
按照这样的规律排列,你认为100第一次出现在( )
第1列 第2列 第3列 第4列
第一行 0
第二行 1 2
第三行 2 3 4
第四行 3 4 5 6
按照这样的规律排列,你认为100第一次出现在( )
| A. | 第50行第50列 | B. | 第50行第51列 | C. | 第51行第50列 | D. | 第51行第51列 |
11.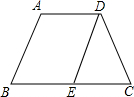 如图,等腰梯形ABCD中,AD∥BC,AD=5,∠B=60°,BC=11,且AB∥DE,△DEC的周长是( )
如图,等腰梯形ABCD中,AD∥BC,AD=5,∠B=60°,BC=11,且AB∥DE,△DEC的周长是( )
 如图,等腰梯形ABCD中,AD∥BC,AD=5,∠B=60°,BC=11,且AB∥DE,△DEC的周长是( )
如图,等腰梯形ABCD中,AD∥BC,AD=5,∠B=60°,BC=11,且AB∥DE,△DEC的周长是( )| A. | 21 | B. | 20 | C. | 19 | D. | 18 |
15.若a、b、c是△ABC的三边的长,化简|a+b-c|+|a+b+c|+|a-b-c|的结果为( )
| A. | a+3b+c | B. | 0 | C. | 3a+b+-c | D. | a+b-c |
5.矩形具有但菱形不具有的性质是( )
| A. | 对角线相等 | B. | 对角线互相垂直 | ||
| C. | 对角线互相平分且相等 | D. | 对角线互相平分 |
12.下列多项式中,能用公式a2±2ab+b2=(a±b)2因式分解的是( )
| A. | x2-xy+y2 | B. | 4a2+2ab+b2 | C. | -a2+2ab-b2 | D. | x2-2y-y2 |
10.下列说法中:①-2是相反数;②2是相反数;③-2是2的相反数;④-2和2互为相反数.其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,△ABC和△ADE都是等边三角形,且点B,A,E在同一直线上,连接BD交AC于M,连接CE交AD于N,连接MN.
如图,△ABC和△ADE都是等边三角形,且点B,A,E在同一直线上,连接BD交AC于M,连接CE交AD于N,连接MN.